Question

A large number of bullets are fired in all directions with the same speed u. What is the maximum area on the ground on which these bullets will spread?
(A). $\pi \dfrac{{{u^2}}}{{{g^2}}}$
(B). $\pi \dfrac{{{u^4}}}{{{g^4}}}$
(C). $\pi \dfrac{{{u^4}}}{{{g^2}}}$
(D).$\pi \dfrac{{{u^3}}}{{{g^2}}}$

Answer 1

Hint: Before attempting this question prior knowledge of the concept of projectile is must, here remember to use $\theta = 4{5^ \circ }$for maximum area on the ground, use this instruction to approach towards the solution.

Complete step-by-step answer:

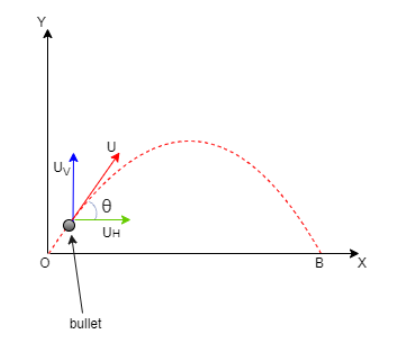
According to the given information we have to find the maximum area covered due to spread of bullets
So we know that the bullets with velocity u projected in all direction
To calculate the maximum area covered by the bullets spread on the ground the bullets need to achieve maximum range
Since the maximum range of a bullet projected at some angle $\theta$ with respect to ground is given by ${R_{\max }} = \dfrac{{{u^2}}}{g}\left( {\sin 2\theta } \right)$
So to achieve maximum range the value of $\sin 2\theta$ should be maximum i.e. 1
$\sin 2\theta = 1$
So we can say that $\sin 2\theta = \sin {90^ \circ }$ (since we know that$\sin {90^ \circ } = 1$)
Therefore $2\theta = {90^ \circ }$
$\Rightarrow$ $\theta = \dfrac{{90}}{2}$ = ${45^ \circ }$
So to achieve maximum range of bullet we need to project the bullet at an angle of ${45^ \circ }$in all direction which has velocity u

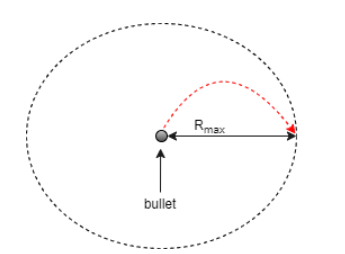
Thus, for the maximum area $\theta$ = ${45^ \circ }$
Maximum range of bullet = ${R_{\max }} = \dfrac{{{u^2}}}{g}\left( {\sin \left( {2 \times 45} \right)} \right)$
$\Rightarrow$ Maximum range of bullet = ${R_{\max }} = \dfrac{{{u^2}}}{g}\left( {\sin {{90}^ \circ }} \right)$
Since $\sin {90^ \circ } = 1$
Therefore Maximum range of bullet = $R = \dfrac{{{u^2}}}{g}$
So the maximum area because of bullets spread on ground = $\pi \times {R_{\max }}^2$
Substituting the given values in the above equation
We get ${A_{\max }} = \pi \times {\left( {\dfrac{{{u^2}}}{g}} \right)^2}$
$\Rightarrow$$${A_{\max }} = \pi \dfrac{{{u^4}}}{{{g^2}}}$So the maximum area on the ground due to bullets spread in all direction is equal to$\pi \dfrac{{{u^4}}}{{{g^2}}}$$
Hence, option C is the correct option.

Note: In the above solution we used the concept of projectile where the object goes under the projectile motion due to the gravitational force acting on the bullet so let’s explain the concept of projectile motion which says that the curved path followed by the object projected obliquely with respect to the surface of the earth with constant acceleration the motion of such bodies is called projectile motion and the path followed by such objects is named as projectile.