Question
Question: A lamina of mass \(M\) in the shape of a quarter of the disc of radius \(R\) as shown in figure. The...
A lamina of mass M in the shape of a quarter of the disc of radius R as shown in figure. The moment of inertia of this lamina about axis AB is (Given C is center of mass)
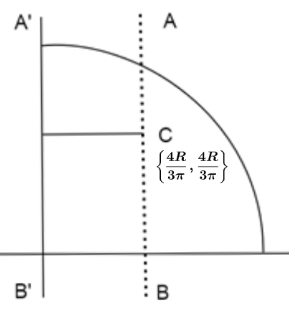
A. MR2(36π29π2−64)
B. MR2(31π29π2+64)
C. MR2(72π210π2−128)
D. MR2(18π29π2−32)
Solution
To find the moment of inertia of the lamina about the given axis, we make use of the concept of parallel axes theorem to find the moment of inertia about a particular axis parallel to the axis of rotation through center of mass.
Complete step by step answer:
The theorem of parallel axes is given by the moment of inertia of a body about any axis is equal to the sum of its moment of inertia about a parallel axis passing through its center of mass and the product of its mass and square of the perpendicular distance between the two axes.i.e.
Idisc=ICOM+Mh2
where, h - perpendicular distance between two axes.
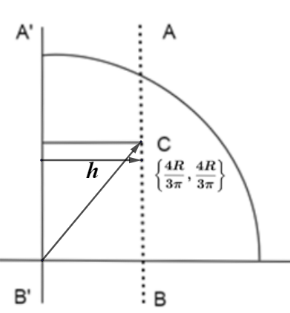
We know that, the moment of inertia of the disc = 2MR2
Then, the moment of inertia of the quarter of the disc Idisc=4MR2
The perpendicular distance between the two axes AB and A′B′ is 2(3π4R) using Pythagoras’ theorem.Now, substituting the values in theorem of parallel axes, we get
\dfrac{{M{R^2}}}{2} = {I_{CM}} + M{\left\\{ {\sqrt 2 \left( {\dfrac{{4R}}{{3\pi }}} \right)} \right\\}^2}
⇒ICM=2MR2−2M(3π4R)2
On solving, we get
∴ICM=MR2(18π29π2−32)
Hence, option D is correct.
Note: The perpendicular distance between the two axes is calculated by using Pythagoras’ theorem taking B′ at origin. We should know the moment of inertia of all the standard bodies. Moment of inertia is directly proportional to mass and the distance between two axes, So, if mass of the body changes, the moment of inertia also changes.
