Question
Question: A lamina is made by removing a small disc of 2R diameter from a bigger disc of uniform mass density ...
A lamina is made by removing a small disc of 2R diameter from a bigger disc of uniform mass density and radius 2R, as shown in figure. The moment of inertia of this lamina about the axis passing through O and P is Io andIp, respectively. Both these axes are perpendicular to the plane of the lamina. The ratio IoIp to the nearest integer is:
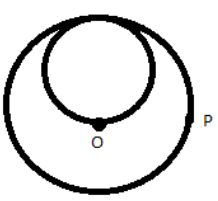
A) 3713
B) 1337
C) 3173
D) 138
Solution
First we found the moment of inertia about O and also found out the moment of inertia about P by subtracting the moment of inertia of cavity from the total part.
Complete step by step solution:
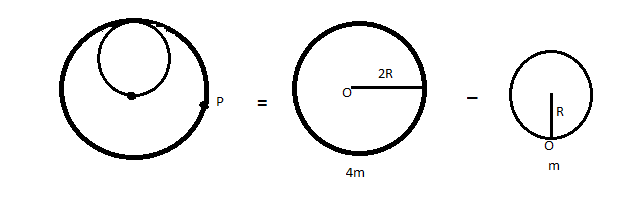
When we rotate this about O, then make a circle of radius 2R. Then first we find the moment of inertia of circle of radius 2Rand subtract moment of inertia of circle of radius R.
I0=21(4m)(2R2)−[21mR2+mR2]
⇒8mR2−23mR2
⇒213mR2
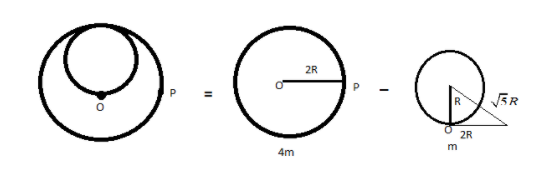
⇒IP=[21(4m)(2R)2+4m(2R)2]−[21mR2+m(5R)2]
⇒[21×4m×4R2+4m×4R2]−[21mR2+5mR2]
⇒[8mR2+16mR2]−[211mR2]
⇒24mR2−211mR2
⇒mR2[24−211]
⇒mR2[248−11]
⇒mR2[237]
⇒237mR2
Then the ratio of moment of inertia around P, to moment of inertia about O.
⇒I0Ip=213237=1337
⇒I0Ip=1337
Note: When we find out the moment inertia around P, then we take a small sphere of radius R, but we should take the sphere radius of 5R.
