Question

A lamina is in the shape of an isosceles trapezium. The parallel sides are 5m apart and their lengths are 3m and 2m. The distance of the center of gravity of the trapezium from the longer of the parallel sides is:
$\begin{aligned} & (A)\dfrac{8}{13}m \\\ & (B)\dfrac{8}{15}m \\\ & (C)6m \\\ & (D)\dfrac{7}{3}m \\\ \end{aligned}$

Answer 1

We will break the trapezoid into two triangles and a rectangle, rather than breaking it vertically or horizontally. This is because the Center of gravity of a rectangle is the midpoint of the rectangle. And since, the other two triangles are right angled triangles, their center of mass will be at their centroids which is at a distance of one by three its base length, one by three its height.

Complete answer:
We will first try to understand how to break down the isosceles trapezium with the following diagram:

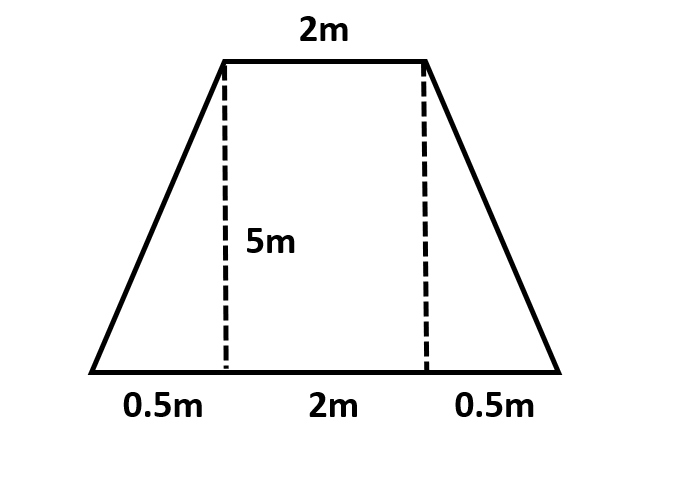
Here, we can see that the two triangles form on the sides of the trapezium and a rectangle is formed in between them.
Now, we need the vertical component of Center of Gravity from the base of this trapezium.
Since, the two triangles are totally identical, they will have the same area and same vertical component of Center of Gravity.
So, let the vertical components of Center of gravity of the two triangles be denoted by ‘y’.
Then,
$\begin{aligned} & \Rightarrow y=\dfrac{\text{height of right-angled triangle}}{3} \\\ & \Rightarrow y=\dfrac{5}{3}m \\\ \end{aligned}$
And, the vertical component of Center of gravity of the rectangle is ‘Y’.
Then,
$\begin{aligned} & \Rightarrow Y=\dfrac{\text{height of rectangle}}{2} \\\ & \Rightarrow Y=\dfrac{5}{2}m \\\ \end{aligned}$
Also, let the areas of the two triangles be “a” and the area of the rectangle be “A”.
Then, we can calculate them as follows:
$\begin{aligned} & \Rightarrow a=\dfrac{1}{2}\times 0.5\times 5 \\\ & \Rightarrow a=\dfrac{5}{4}{{m}^{2}} \\\ \end{aligned}$
And,
$\begin{aligned} & \Rightarrow A=5\times 2 \\\ & \Rightarrow A=10{{m}^{2}} \\\ \end{aligned}$
Then, the distance of Center of gravity of the trapezium from the base will be equal to:
$\Rightarrow {{Y}_{COG}}=\dfrac{ay+AY+ay}{a+A+a}$
Putting the values of all the respective terms, we get:
$\begin{aligned} & \Rightarrow {{Y}_{COG}}=\dfrac{\dfrac{5}{4}\times \dfrac{5}{3}+10\times \dfrac{5}{2}+\dfrac{5}{4}\times \dfrac{5}{3}}{\dfrac{5}{4}+10+\dfrac{5}{4}} \\\ & \Rightarrow {{Y}_{COG}}=\dfrac{350}{150} \\\ \end{aligned}$
$\therefore {{Y}_{COG}}=\dfrac{7}{3}m$
Hence, the center of gravity of the isosceles trapezium from the longer base comes out to be $\dfrac{7}{3}m$ .

Hence, option (D) is the correct option.

Note:
Since an isosceles triangle is symmetric along the vertical axis. Therefore, we can say that the center of gravity of the whole trapezium would lie somewhere on this axis. We can always use these simple facts in problems, that is, if it were asked the distance of center of mass from the ends of the trapezium.