Question

A lady walks on a level road at ${\text{3}}\,km/hr{\text{ }}$in rain. Raindrops fall vertically through the air at $4\,km/hr$. At what angle she should hold her umbrella to protect herself from the rain?

Answer 1

Using vector analysis, know the direction of rain with respect to the direction of ground. Make the geometric construction of the velocities of the lady and rain with respect to ground. Find the angle between velocity of rain with respect to lady and ground.

Complete step by step answer:
The given question is on the relative velocity. The following figure will ease my understanding of the problem.

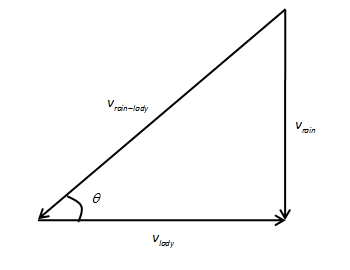
In the above diagram, ${v_{lady}}$is the velocity of the lady walking on the level road, ${v_{rain}}$ is the velocity of the rain, and ${v_{rain - lady}}$ is the velocity of the rain with respect to the lady. The direction of ${v_{rain - lady}}$ is the direction of the rain drops falling on the lady as she also moves with velocity ${v_{lady}}$. Therefore, she has to hold her umbrella at angle $\theta$ from the level road.

The real life example of relative motion is when we travel through a boat in a river. Suppose the boat is moving from west to east direction, across the river and the river is also flowing from south to north, then the boat eventually is moving north-east.

We can calculate the angle $\theta$ using trigonometry, as $\tan \theta$ is equal to the opposite side divided by the adjacent side. Therefore,
$\tan \theta = \dfrac{{{v_{rain}}}}{{{v_{lady}}}}$
$\Rightarrow \theta = {\tan ^{ - 1}}\left( {\dfrac{{{v_{rain}}}}{{{v_{lady}}}}} \right)$

Substitute $4\,km/hr$ for ${v_{rain}}$ and $3\,km/hr$ for ${v_{lady}}$ in the above equation.
$\theta = {\tan ^{ - 1}}\left( {\dfrac{{4\,km/hr}}{{3\,km/hr}}} \right)$
$\theta = 53^\circ$

Therefore, the lady has to hold her umbrella at $53^\circ$ from the road or $90^\circ - 53^\circ = 37^\circ$ from the vertical direction.

Note:
For the given problem, we don’t need to determine the velocity of the rain with respect to the lady as the rain is falling vertically straight downward. If the direction of rain is not perpendicular to the level ground, we are forbidden to use the formula $\tan \theta = \dfrac{{{v_{rain}}}}{{{v_{lady}}}}$ as it is not the right-angle triangle.