Question

A ladder rests against a frictionless vertical wall, with its upper end 6 m above the ground and the lower end 4 m away from the wall. The weight of the ladder is 500 N and its center of gravity at $\left( {1/3} \right)rd\;$ distance from the lower end. Wall's reaction will be, in N
A) 111
B) 333
C) 222
D) 129

Answer 1

In this solution, we will calculate the components that will contribute to the torque of the ladder. Since the ladder is stationary, the net torque of the ladder will be zero. The reaction of the wall will be balanced by the

Complete step by step answer:
We’ve been given that a ladder rests on a frictionless wall such that its centre of gravity is $\left( {1/3} \right)rd\;$ a distance from the lower end. Then the ladder will be at rest only if the ladder experiences a friction force from the ground. Let us start by forming a free body diagram of the system.

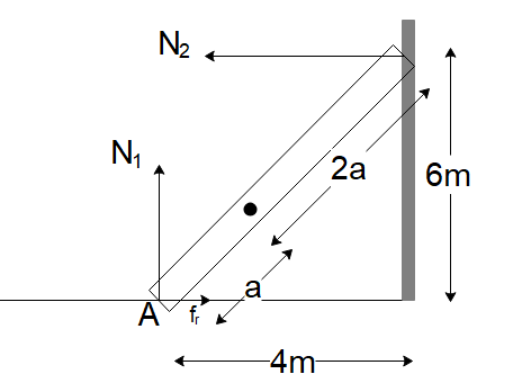
Since the ladder is in equilibrium, the net forces on it will be zero. Hence in the vertical direction, we can see that the normal force ${N_1}$ will be balanced by the weight of the ladder. So, we can write
${N_1} = 500\,N$
For the ladder to be in equilibrium, the torque of the ladder must also be zero from any point. Let us calculate the torque of the ladder about point A.
The length of the ladder will be determined from Pythagoras’s theorem as
$l = \sqrt {{4^2} + {6^2}} = \sqrt {52}$
Now the forces that will contribute to the torque on the ladder will be

1. weight of the ladder making it want to rotate clockwise
2. normal reaction of the wall on the ladder making the ladder want to rotate anticlockwise
   Then we can balance the torque due to these forces since the ladder is stationary. The weight of the rod acts on the centre of the mass of the ladder. Since we’re calculating the torque of the ladder about point A, the distance of the centre of mass of the rod from the point will be $\dfrac{{\sqrt {52} }}{3}$.
   Then the torque due to the 1st force will be ${\tau _1} = - 500 \times \dfrac{{\sqrt {52} }}{3}\cos \theta$. (negative because it acts in the clockwise direction)
   $\cos \theta$ can be determined from the trigonometry of the situation as $\cos \theta = \dfrac{4}{{\sqrt {52} }}$. So,
   ${\tau _1} = - 500 \times \dfrac{{\sqrt {52} }}{3} \times \dfrac{4}{{\sqrt {52} }}$
   $\Rightarrow {\tau _1} = - 2000/3$
   The torque due to the second force will be
   ${\tau _2} = {N_2} \times 6$
   Since the net torque is zero, we can write
   ${\tau _1} + {\tau _2} = 0$
   Which gives us
   $- \dfrac{{2000}}{3} + 6{N_2} = 0$
   Which gives us
   ${N_2} \approx 111\,N$

Hence the correct choice is option (A).

Note: While calculating the torque about any point, we must take the component of the length that is perpendicular to the force. So for the first force, we take the horizontal component of length and for the second force, we take the vertical component of length which is 6 meters as the force is horizontal.