Question

A ladder leans against a wall making an angle of $60^\circ$ to the ground and reaches the height 10 m on the wall. Find the length of the ladder and the distance between the lower end of the ladder and the base of the wall.

Answer 1

Here, we need to find the length of the ladder and the distance between the lower end of the ladder and the base of the wall. We will use the formula for sine of the given angle, and simplify the equation to get the length of the ladder. Then, we will use the formula for cosine of the given angle, and simplify the equation to get the distance between the lower end of the ladder and the base of the wall.

Formula Used: We will use the following formula to solve the question:
1.The sine of an angle $\theta$ of a right angled triangle, $\sin \theta = \dfrac{{{\rm{Perpendicular}}}}{{{\rm{Hypotenuse}}}}$.
2.The cosine of an angle $\theta$ of a right angled triangle, $\cos \theta = \dfrac{{{\rm{Base}}}}{{{\rm{Hypotenuse}}}}$.

Complete step-by-step answer:
First, we will draw the diagram using the given information.

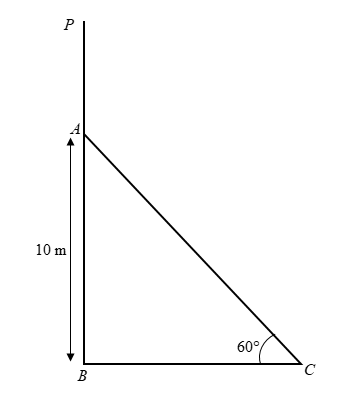
Here, $AC$ is the ladder and $PB$ is the wall. The ladder touches the wall at the height of $AB = 10{\rm{ m}}$. The distance between the lower end of the ladder and the base of the wall is $BC$.
We will use trigonometric ratios to find the length of the ladder and the distance between the lower end of the ladder and the base of the wall.
Now, we can observe that the triangle $ABC$ is right angled at $\angle B$.
We know that the sine of an angle $\theta$ of a right angled triangle is given by $\sin \theta = \dfrac{{{\rm{Perpendicular}}}}{{{\rm{Hypotenuse}}}}$.
Therefore, we get the sine of $\angle C$ as
$\sin \angle C = \dfrac{{AB}}{{AC}}$
Substituting $\angle C = 60^\circ$ and $AB = 10{\rm{ m}}$ in the equation, we get
$\Rightarrow \sin 60^\circ = \dfrac{{10}}{{AC}}$
We know that the sine of angle $60^\circ$ is equal to $\dfrac{{\sqrt 3 }}{2}$.
Substituting $\sin 60^\circ = \dfrac{{\sqrt 3 }}{2}$, we get
$\Rightarrow \dfrac{{\sqrt 3 }}{2} = \dfrac{{10}}{{AC}}$
Simplifying the expression, we get
$\begin{array}{l} \Rightarrow \sqrt 3 \times AC = 2 \times 10\\\ \Rightarrow AC = \dfrac{{20}}{{\sqrt 3 }}{\rm{ m}}\end{array}$
Rationalising the expression, we get
$\begin{array}{l} \Rightarrow AC = \dfrac{{20}}{{\sqrt 3 }} \times \dfrac{{\sqrt 3 }}{{\sqrt 3 }}{\rm{ m}}\\\ \Rightarrow AC = \dfrac{{20\sqrt 3 }}{3}{\rm{ m}}\end{array}$
Therefore, the length of the ladder is $\dfrac{{20\sqrt 3 }}{3}$ m.
Now, we will find the distance between the lower end of the ladder and the base of the wall.
We know that the cosine of an angle $\theta$ of a right angled triangle is given by $\cos \theta = \dfrac{{{\rm{Base}}}}{{{\rm{Hypotenuse}}}}$.
Therefore, we get the cosine of $\angle C$ as
$\cos \angle C = \dfrac{{BC}}{{AC}}$
Substituting $\angle C = 60^\circ$ and $AC = \dfrac{{20\sqrt 3 }}{3}{\rm{ m}}$ in the equation, we get
$\Rightarrow \cos 60^\circ = \dfrac{{BC}}{{\dfrac{{20\sqrt 3 }}{3}}}$
Simplifying the expression, we get
$\Rightarrow \cos 60^\circ = \dfrac{{3BC}}{{20\sqrt 3 }}$
We know that the cosine of angle $60^\circ$ is equal to $\dfrac{1}{2}$.
Substituting $\cos 60^\circ = \dfrac{1}{2}$, we get
$\Rightarrow \dfrac{1}{2} = \dfrac{{3BC}}{{20\sqrt 3 }}$
Simplifying the expression, we get
$\begin{array}{l} \Rightarrow 20\sqrt 3 = 2 \times 3BC\\\ \Rightarrow 20\sqrt 3 = 6BC\end{array}$
Dividing both sides by 6, we get
$\begin{array}{l} \Rightarrow \dfrac{{20\sqrt 3 }}{6} = \dfrac{{6BC}}{6}\\\ \Rightarrow BC = \dfrac{{10\sqrt 3 }}{3}{\rm{ m}}\end{array}$
Therefore, the distance between the lower end of the ladder and the base of the wall is $\dfrac{{10\sqrt 3 }}{3}$ m.

Note: We can use the angle sum property to find the other angle and use the sine of that angle to find the distance between the lower end of the ladder and the base of the wall.
The angle sum property of a triangle states that the sum of the three interior angles of a triangle is always $180^\circ$.
Therefore, in triangle $ABC$, we get
$\angle ABC + \angle BAC + \angle BCA = 180^\circ$
Substituting $\angle ABC = 90^\circ$ and $\angle BCA = 60^\circ$, we get
$\begin{array}{l} \Rightarrow 90^\circ + \angle BAC + 60^\circ = 180^\circ \\\ \Rightarrow 150^\circ + \angle BAC = 180^\circ \end{array}$
Subtracting $150^\circ$ from both sides, we get
$\angle BAC = 30^\circ$
Now, we get the sine of $\angle BAC$ as
$\sin \angle BAC = \dfrac{{BC}}{{AC}}$
Substituting $\angle BAC = 30^\circ$ and $AC = \dfrac{{20\sqrt 3 }}{3}{\rm{ m}}$ in the equation, we get
$\Rightarrow \sin 30^\circ = \dfrac{{BC}}{{\dfrac{{20\sqrt 3 }}{3}}}$
Rewriting the expression, we get
$\Rightarrow \sin 30^\circ = \dfrac{{3BC}}{{20\sqrt 3 }}$
We know that the sine of angle $30^\circ$ is equal to $\dfrac{1}{2}$.
Substituting $\sin 30^\circ = \dfrac{1}{2}$, we get
$\Rightarrow \dfrac{1}{2} = \dfrac{{3BC}}{{20\sqrt 3 }}$
Simplifying the expression, we get
$\begin{array}{l} \Rightarrow 20\sqrt 3 = 2 \times 3BC\\\ \Rightarrow 20\sqrt 3 = 6BC\end{array}$
Dividing both sides by 6, we get
$\begin{array}{l} \Rightarrow \dfrac{{20\sqrt 3 }}{6} = \dfrac{{6BC}}{6}\\\ \Rightarrow BC = \dfrac{{10\sqrt 3 }}{3}{\rm{ m}}\end{array}$
$\therefore$ The distance between the lower end of the ladder and the base of the wall is $\dfrac{{10\sqrt 3 }}{3}$ m.