Question

A ladder, 5-meter-long, standing on a horizontal floor, leans against a vertical wall. If the top of the ladder slides downwards at the rate of 10 cm/sec, then the rate at which the angle between the floor and the ladder is decreasing when lower end of ladder is 2 metres from the wall is:

Answer 1

To solve the given problem, we will apply the use of trigonometrical properties related to height and distance. Also, the rate of sliding (movement) should be used to determine the rate of decreasing angle, using the method of derivatives.

Complete step-by-step answer:

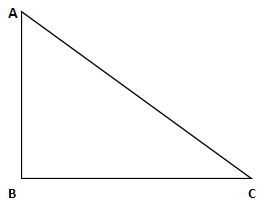
Let us consider the above $\vartriangle ABC$, right angled at B.
In the above diagram, the right angle is at angle B and let the angle between floor and ladder be $\theta$

Let at any time ‘t’, AB = x cm, BC = y cm and we know AC = 500 cm
$\therefore \sin \theta =\dfrac{x}{500}$
$\Rightarrow x=500\sin \theta$
and
$\cos \theta =\dfrac{y}{500}$
$y=500\cos \theta$
Also, it is given that
$\dfrac{\mathrm{d} x}{\mathrm{d} t}=10cm/s \Rightarrow \dfrac{\mathrm{d} (500\sin \theta )}{\mathrm{d} t} = 10cm/s \Rightarrow 500.\cos \theta .\dfrac{\mathrm{d} \theta }{\mathrm{d} t}=10cm/s \Rightarrow \dfrac{\mathrm{d} \theta }{\mathrm{d} t}=\dfrac{1}{50\cos \theta }$
For y = 2m = 200 cm,
$\dfrac{\mathrm{d} \theta }{\mathrm{d} t} = \dfrac{1}{50\ast \dfrac{y}{500}} = \dfrac{10}{y} = \dfrac{10}{200} = \dfrac{1}{20}rad/s$

Note: Based on the given values in the problem, appropriate trigonometric functions should be used. The unit of conversion has to be taken into consideration, as this might lead to incorrect output.
For the rate change, we have applied the rules of derivatives, where the implicit derivative rule has been applied using a chain method. The dependent and independent variables should also be taken care of. The rate of change with respect to speed is provisioned with the rate of change of angle.