Question

A ladder 15 meters long reaches the top of a vertical wall. If the ladder makes an angle of ${{60}^{\circ }}$ with the wall, find the height of the wall.

Answer 1

Hint:Considering the length of the ladder i.e 15 meters as Hypotenuse side and $\theta$ be the angle made by ladder with wall.We will apply the formula of trigonometric ratios of cosine. And this formula is given by $\cos \left( \theta \right)=\dfrac{\text{Adjacent side}}{\text{Hypotenuse}}$.The length of the adjacent side gives the height of the wall.

Complete step-by-step answer:
We have been given a ladder of 15 meters long that reaches the top of the vertical wall and makes an angle of${{60}^{\circ }}$ with the wall. Let us suppose the ladder to be AB that reaches the top of a vertical wall and join the bottom of the ladder to the wall such that it forms a right angled triangle at C.

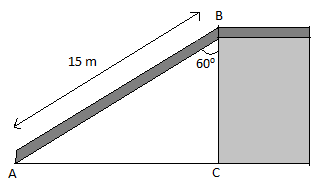
Now we have to find BC which is equal to the height of the wall.
In $\Delta ABC$ we will consider,
$\cos B=\dfrac{BC}{AB}$
Since we have to find the length BC and AB have been given to us which is equal to the length of the ladder i.e. 15 m. So we used the cosine which means ratio of base to hypotenuse of the right angle triangle. Also, $\angle B={{60}^{\circ }}$.
$\Rightarrow \cos {{60}^{\circ }}=\dfrac{BC}{15}$
We know that $\cos {{60}^{\circ }}=\dfrac{1}{2}$
$\Rightarrow \dfrac{1}{2}=\dfrac{BC}{15}$
On cross multiplication, we get as follows:
$\Rightarrow 2BC=15$
On dividing the above equation by 2 on both sides, we get as follows:

& \Rightarrow \dfrac{2BC}{2}=\dfrac{15}{2} \\\ & \Rightarrow BC=7.5m \\\ \end{aligned}$$ Therefore, the height of the wall is equal to 7.5 m. Note: In this type of question, you must have to draw a diagram according to the condition given in the question and then move further for calculation. Also, be careful while drawing the diagram and mark the angle correctly according to the question. For example, if you mark angle A as 60 degrees, then we will get an incorrect answer as in question they said angle is made with the wall not with the ground.So we have to take with respect to wall .Also, don’t get confused about the value of $$\cos {{60}^{\circ }}$$. Sometimes we use $$\cos {{60}^{\circ }}=\dfrac{\sqrt{3}}{2}$$ by mistake, which is wrong as we know that $$\cos {{60}^{\circ }}=\dfrac{1}{2}$$. Students should remember the important trigonometric ratios and standard angles to solve these types of questions.