Question

A kite is flying at a height of 75 meters from the ground level, attached to a string inclined at ${{60}^{\circ }}$ to the horizontal. Find the length of the strings to the nearest meter.

Answer 1

Hint:In the above question first of all we will suppose a kite along with the string AB where A is the kite and B represents the end point of the string which is inclined at ${{60}^{\circ }}$ to the horizontal. Then we will use the trigonometric ratio to find the length of the strings.

Complete step-by-step answer:
We have been given a kite flying at a height of 75 meters from the ground level and attached to a string inclined at ${{60}^{\circ }}$ to the horizontal.
Let us suppose the kite along with the strings to be AB such that A is a kite and B is the end point of the strings which is inclined at ${{60}^{\circ }}$to the horizontal.
Also, we have been given the height of the point A to be 75 meters.

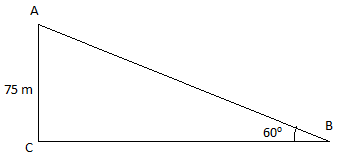
Let us consider triangle ABC,where AB be the length of string and AC be the height of the kite.Then applying trigonometric ratio we get,
$\sin B=\dfrac{AC}{AB}$
Since we know that sine of any angle in a right angled triangle is equal to the ratio of perpendicular is to hypotenuse of the triangle.
Also, we have $\angle B={{60}^{\circ }}$ and AC = 75m.
$\Rightarrow \sin {{60}^{\circ }}=\dfrac{75}{AB}$
We know that $\sin {{60}^{\circ }}=\dfrac{\sqrt{3}}{2}$
$\Rightarrow \dfrac{\sqrt{3}}{2}=\dfrac{75}{AB}$
On cross multiplication, we get as follows:

& AB\sqrt{3}=75\times 2 \\\ & \Rightarrow AB\sqrt{3}=150 \\\ \end{aligned}$$ On dividing both sides by $$\sqrt{3}$$, we get as follows: $$\begin{aligned} & \dfrac{AB\sqrt{3}}{\sqrt{3}}=\dfrac{150}{\sqrt{3}} \\\ & \Rightarrow AB=\dfrac{150}{\sqrt{3}} \\\ \end{aligned}$$ On rationalizing the denominator by multiplying numerator as well as denominator by $$\sqrt{3}$$ we get as follows: $$\begin{aligned} & AB=\dfrac{150\times \sqrt{3}}{\sqrt{3}\times \sqrt{3}} \\\ & AB=\dfrac{150\sqrt{3}}{3} \\\ & \Rightarrow AB=50\sqrt{3} \\\ \end{aligned}$$ We know that $$\sqrt{3}=1.732$$ $$\begin{aligned} & \Rightarrow AB=50\times 1.732 \\\ & \Rightarrow AB=86.60m \\\ \end{aligned}$$ We have been asked to find the length of string to the nearest meter. Therefore, the length of the string is equal to 87 m. Note: In this type of question you must have to draw a diagram according to the condition given in the question and then move further to calculation. Also, be careful while drawing the diagram and mark the angle correctly according to the question otherwise we will get incorrect answers. Also, don’t get confused in the value of $$\sin {{60}^{\circ }}=\dfrac{1}{2}$$ which is wrong as we know $$\sin {{60}^{\circ }}=\dfrac{\sqrt{3}}{2}$$.We can also use other trigonometric ratios i.e $\tan$ ,$\cos$ ,$\textrm{cosec}$ to solve this question, we get one unknown value and consider it as one equation and use another trigonometric ratio equate it to the first equation,by simplifying and using standard angles we get the same answer.