Question

A kite is flying at a height of $60m$ above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is ${60^ \circ }$ . Find the length of the string, assuming that there is no slack in the string.

Answer 1

In order to solve this question, we need to analyse the information given in the question. After that, we will be able to form a figure which is a right-angled triangle. After that, by using the basic trigonometric ratios, we can solve this question.

Complete step-by-step answer:
Let us first understand the question. A kite is flying at a height of $60m$ which means that the perpendicular distance between the kite and the ground is $60m$.
It is attached to a string with inclination ${60^ \circ }$ which means that the angle between the string attached to the kite and the string is ${60^ \circ }$. After understanding the question and analysing the situation, we can clearly see that the figure formed by analysing the situation is a right-angled triangle as shown

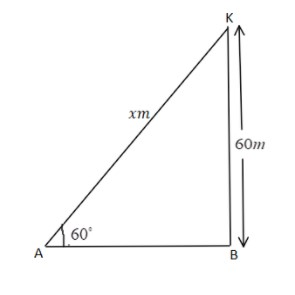
Now, we need to find out the length of the string.
Let us assume that the length of the string holding the kite is $x{\text{ }}m$ .
Now we can easily find out the value of $x$ by using the basic trigonometric ratio.
$\sin \theta = \dfrac{{{\text{Perpendicular}}}}{{{\text{Hypotenuse}}}}$ , we get
$\sin {60^ \circ } = \dfrac{{60}}{x}$
Now the value of $\sin {60^ \circ }$ is $\dfrac{{\sqrt 3 }}{2}$
$\Rightarrow \dfrac{{\sqrt 3 }}{2} = \dfrac{{60}}{x} \\\ \Rightarrow x = \dfrac{{120}}{{\sqrt 3 }} = \dfrac{{120\times\sqrt 3}}{{\sqrt 3\times\sqrt 3 }}= \dfrac{{120\times\sqrt 3}}{3} = 40\sqrt 3 m \\\$
Therefore, length of the string is $40\sqrt 3 m$

Note: For solving these kind of practical trigonometric equations , the key is to imagine the situation carefully and draw the diagram according to given information in question.Also students should remember the trigonometric ratios , formulas and identities for solving these types of problems.