Question

A kite is $300\,m$ high and there are $500\,m$ of cord out. If the wing moves the kite horizontally at the rate of $5$ kilometres per hour directly away from the person who is flying it, the rate at which the cord is being paid is?
A. $2$ kilometres per hour
B. $4$ kilometres per hour
C. $6$ kilometres per hour
D. $8$ kilometres per hour

Answer 1

The kite has a certain height, and the cord extends to a certain height, as mentioned in the question. We must now determine the rate at which the cord is being paid out if the kite is flying horizontally at a speed of five kilometres per hour. First, we'll figure out the height-cord equation, and then we'll figure out the pace by differentiating the obtained equation.

Complete step by step answer:
We are given that a kite is flying at $300\,m$ height and length of cord that is out is $500\,m$. We know that the height of cord, the length of cord and the base of ground makes a right angled triangle as shown in the figure below.

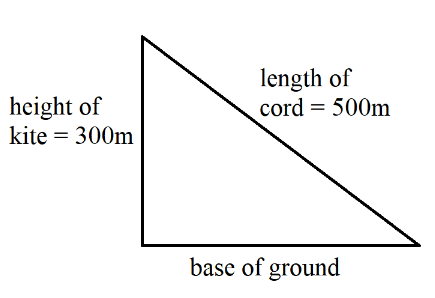
So, we use the Pythagoras theorem in the right angled triangle,
${h^2} + {b^2} = {l^2} - - - - \left( 1 \right)$
where h is the height of the kite, b is the base of the ground and l is the length of the cord.
So, we first calculate the value of distance of base of ground from person to the kite.
So, substituting the value of height of kite and length of cord, we get,
$\Rightarrow {\left( {300m} \right)^2} + {b^2} = {\left( {500m} \right)^2}$
Shifting the terms of the equation and computing the square of terms, we get,
$\Rightarrow {b^2} = {\left( {500m} \right)^2} - {\left( {300m} \right)^2}$
$\Rightarrow {b^2} = 250000\,{m^2} - 90000\,{m^2}$
$\Rightarrow {b^2} = 160000\,{m^2}$
Taking square root on both sides of the equation and considering only the positive value as length cannot be negative.
$\Rightarrow b = 400m$

Now differentiating the equation $\left( 1 \right)$ using the chain rule of differentiation, we get,
$\Rightarrow 2h\dfrac{{dh}}{{dt}} + 2b\dfrac{{db}}{{dt}} = 2l\dfrac{{dl}}{{dt}}$
Now, we height of kite $= h = 300\,m$
Length of cord $= l = 500\,m$
Distance along base of ground from person to kite $= b = 400\,m$
Also, the speed of kite horizontally away from the person$= \dfrac{{db}}{{dt}} = 5kmph = \dfrac{{5000m}}{{1hr}}$
Since the height of the kite remains constant. Hence, we have, $\dfrac{{dh}}{{dt}} = 0kmph = \dfrac{{0m}}{{1hr}}$.
We have to find the value of $\dfrac{{dl}}{{dt}}$ from the equation.
Now, substituting the value of the known quantities in the equation, we get,
$2\left( {300m} \right)\left( {\dfrac{{0m}}{{1hr}}} \right) + 2\left( {400m} \right)\left( {\dfrac{{5000m}}{{1hr}}} \right) = 2\left( {500m} \right)\left( {\dfrac{{dl}}{{dt}}} \right)$

Simplifying the equation, we get,
$\Rightarrow 800 \times 5000 = 1000\left( {\dfrac{{dl}}{{dt}}} \right)$
Dividing both sides of the equation by $1000$, we get,
$\Rightarrow 800 \times 5 = \left( {\dfrac{{dl}}{{dt}}} \right)$
$\therefore \left( {\dfrac{{dl}}{{dt}}} \right) = 4000$
Therefore, we get a rate at which the card is being paid as $4000$ metres per hour or $4$ kilometres per hour. So, actually if the wind moves the kite horizontally at the rate of $5$ kilometres per hour directly away from the person who is flying it, the rate at which the cord is being paid is $4$ kilometres per hour.

Hence, the correct answer is option B.

Note: While taking derivative, we know the power rule of differentiation as $\dfrac{{d\left( {{x^n}} \right)}}{{dx}} = n{x^{\left( {n - 1} \right)}}$ where x is variable and n is constant. We must know the chain rule of differentiation to form the equation required for getting to the final answer. We also should know the applications of Pythagoras theorem in order to calculate the third side of the right angled triangle.