Question

A kite is 120m high and 130m string is out. If the kite is moving away horizontally at the ratio of $52{\text{ }}m/s$ find the rate at which the string is being paid out.

Answer 1

The given question is that the kite is having some specific height and the string is out to some height. If the kite is moving horizontally at the rate of some height now we have to find out the rate at which the string is being paid out. Firstly we will find out the equation relating height and string then further find out the rate.

Complete step-by-step answer:
We are given that a kite is flying at $120m$ height and the string is out $130m$. Therefore a figure can be made

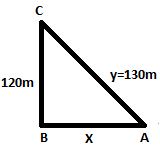
Here BC is the height of the kite. So $BC = 120m$ and we suppose $AC = ym$ and $BA = x$ metre
Therefore, we can apply Pythagoras theorem in the above right angled triangle
$\Rightarrow {y^2} = {x^2} + {(120)^2} - - - - - - - (i)$
Now it is given that kite is moving away horizontally at the rate of $52{\text{ }}m/s$
Which means $\dfrac{{dx}}{{dt}} = 52m/s - - - - - - - - (ii)$
Where $\dfrac{{dx}}{{dt}}$ is rate of horizontal movement of kite which is equal to $52{\text{ }}m/s$
Since $\dfrac{{dx}}{{dt}}$ is given, One another $\dfrac{{dx}}{{dt}}$ can also be found by differentiating $(i)$ with respect to time. So differentiating 1 w.r.t ‘$t$’, we get
$\Rightarrow 2y\dfrac{{dy}}{{dt}} = 2x\dfrac{{dx}}{{dt}} + 0 - - - - - - - - (iii)$
Where $\dfrac{d}{{dt}}({x^2}) = 2x\dfrac{{dx}}{{dt}},\dfrac{d}{{dt}}({y^2}) = 2y\dfrac{{dy}}{{dt}}$and $\dfrac{d}{{dt}}{(120)^2} = 0$because derivative of constant is zero and $\dfrac{d}{{dt}}({x^n}) = n{x^{n - 1}}\dfrac{{dx}}{{dt}}$
From $(iii)$we get
$\Rightarrow 2y\dfrac{{dy}}{{dt}} = 2x\dfrac{{dx}}{{dt}}$
$2$ get cancel on both sides
\Rightarrow $$$$y\dfrac{{dy}}{{dt}} = x\dfrac{{dx}}{{dt}}
\Rightarrow $$$$\dfrac{{dy}}{{dt}} = \dfrac{x}{y}\dfrac{{dx}}{{dt}}
From $(ii)$ putting the value $\dfrac{{dx}}{{dt}}$ = $52{\text{ }}m/s$. Here and we get
$\Rightarrow \dfrac{{dy}}{{dt}} = \dfrac{x}{y}(52)$
Also given $y{\text{ }} = {\text{ }}130m$ and $x{\text{ }} = {\text{ }}50m$
Putting here the values of $x$ and $y$, we get
$\Rightarrow \dfrac{{dy}}{{dt}} = \dfrac{{50}}{{130}}(52)$
On solving, we get
$\Rightarrow \dfrac{{dy}}{{dt}} = 20m/s$
Therefore, string is paid at the rate of $20m/s$ where $x{\text{ }} = {\text{ }}50$ was found by using Pythagoras theorem in given right angled triangle
Which means ,
$\Rightarrow A{C^2} = A{B^2} + B{C^2}$
$\Rightarrow {(130)^2} = {(AB)^2} + {(120)^2}$
$\Rightarrow 16900 = {(AB)^2} + 14400$
From her, $AB{\text{ }} = {\text{ }}x$ mitre
$\Rightarrow 16900{\text{ }} = {\text{ }}{x^2} + 14400$
From the above equation, value of $x$ can be found
$\Rightarrow 16900{\text{ }} = {\text{ }}{x^2} + 14400$
On taking square root, we get
$\Rightarrow {x^2} = 16900 - 14400$
$\Rightarrow {x^2} = 2500$
$x = 50m$
Therefore we took $x$ as $50m$

Note: While taking derivative, we know the formula of derivative of variable to the power constant is $\dfrac{d}{{dt}}({x^n}) = n{x^{n - 1}}$ where $x$ is variable and $n$ is constant and here the derivative of variable to the power constant with respect to an another variable is$\dfrac{d}{{dt}}({x^n}) = n{x^{n - 1}}\dfrac{{dx}}{{dt}}$ where $t$, $x$ are variables and$n$is constant. Here an extra term $\dfrac{{dx}}{{dt}}$is there because two variables are different.