Question

A kite is 120 ft high when 650ft of string is out. What angle does the kite make with the ground assuming the string is directly tethered to the ground?

Answer 1

Now to solve the problem we will first draw the figure of the given conditions. Now we want to find the angle made by the kite and the ground. Now take the sin ratio of the angle and hence substitute the values in the ratio. Now take ${{\sin }^{-1}}$ and solve the problem.

Complete step by step solution:
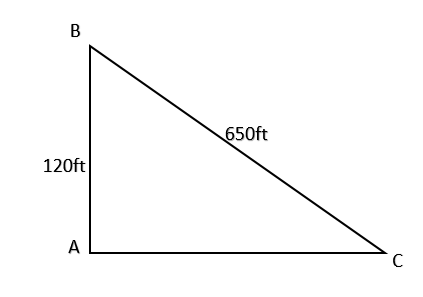
Now let us first draw the figure of the given conditions.
Now let B be the point which represents the kite.
Let the string be CB, we know that the length of string is 650ft. Hence the length of CB is 650ft.
Now let A be the point on the ground such that BA is perpendicular to AC.
Now we are given that the distance between the kite is 120ft above the ground.
Hence AB = 120ft

Now we want to find the angle the kite makes from the ground.
Hence we want to find the angle C.
Now let us say $\angle C=\theta$
Now we know that $\sin \theta =\dfrac{\text{opposite}}{\text{hypotenuse}}$ .
Hence we have, $\sin \theta =\dfrac{120}{650}=\dfrac{12}{65}$
Hence we have $\sin \theta =\dfrac{12}{65}$.
Hence we can say that the angle $\theta ={{\sin }^{-1}}\left( \dfrac{12}{65} \right)$
Hence the kite makes angle $\theta ={{\sin }^{-1}}\left( \dfrac{12}{65} \right)$ from the ground.

Note:
Now note that the distance of the kite from the ground is always given as a perpendicular distance. Hence in such scenarios we always get a right angle triangle and then the angle can always be found by choosing the appropriate trigonometric ratio.