Question
Question: A junction diode has a resistance \(25\,\Omega \) when forward biased and \(2500\,\Omega \) reverse-...
A junction diode has a resistance 25Ω when forward biased and 2500Ω reverse-biased. What will be the current in the diode for the arrangement shown?
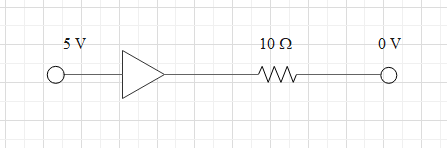
A. 151A
B. 71A
C. 251A
D. 1801A
Solution
When the positive terminal of a diode is connected to a high voltage and the negative terminal is connected to a low voltage then the diode is forward biased. When connected in the forward bias it allows current to pass through it. Here, since the diode and resistor are connected in series the total resistance is given by the sum of resistance offered by them. If we know the total resistance current can be calculated by dividing voltage by total resistance.
Complete step by step answer:
A diode is a semiconductor device used to control current in an electric circuit. A diode has two terminals: a positive terminal and a negative terminal. When the positive terminal of a diode is connected to a high voltage and the negative terminal is connected to a low voltage then the diode is forward biased. When connected in the forward bias it allows current to pass through it.
When the positive terminal of the diode is connected to a low voltage and the negative terminal of the diode is connected to a high voltage then the diode is said to be reverse biased. When connected in reverse bias the diode will not allow the flow of current.
In the given arrangement we can see that the positive terminal of the diode is connected to a high voltage of 5Ω, and the negative terminal is connected to a low voltage of 0Ω. This means the diode is forward biased. Hence it allows the current to pass through it.
It is given that resistance of junction diode when forward biased,
Rf=25Ω
When resistors are connected in series the total resistance is given by the sum of resistance offered by the resistors.
Thus, the total resistance in the given arrangement can be calculated as
RTotal=Rf+R
Where R is the resistance of the resistor. We can see a resistance of 10Ω is connected in series to the diode.
Now substitute the values
RTotal=25Ω+10Ω=35Ω
From ohm's law, we know that voltage is directly proportional to current. The relation between voltage and current is given as
V=IR
Thus, the current can be calculated by dividing voltage by resistance.
I=RV
Voltage,
V=5V−0V=5V
Substitute the values we get,
I=RV
⇒I=35Ω5V
∴I=71A
Therefore, the current in the diode is 71A. Hence, the correct option is (B).
Note:
When the positive terminal of a diode is connected to a high voltage and the negative terminal is connected to a low voltage then the diode is forward biased. When connected in the forward bias it allows current to pass through it. Always check the biasing condition before answering. If it was reverse biased the answer would be zero since the diode will not conduct in reverse bias.
