Question

A juggler maintains 10 balls in motion, making each of them rise at a height of $80{\text{m}}$ from his hands. Find the time interval maintained by the juggler to keep the proper distance between them.
A) $0 \cdot 6{\text{s}}$
B) $0 \cdot 8{\text{s}}$
C) $1 \cdot 0{\text{s}}$
D) $1 \cdot 2{\text{s}}$

Answer 1

Here when one ball leaves the hand of the juggler and returns to his hand, the next ball will leave the juggler’s hand. So if we obtain the total time taken for one ball to leave the juggler’s hand and return to his hand, then dividing that value by the number of balls will give us the time interval maintained by the juggler. We can employ Newton’s second and third equations of motion for either the ascent of the ball or its descent to obtain the time taken for one ball to go up and come down to the juggler’s hand.

Formulas used:
-Newton’s third equation of motion is given by, ${v^2} = {u^2} + 2as$ where $v$ is the final velocity of the body, $u$ is its initial velocity, $a$ is the acceleration and $s$ is the displacement of the body.
-Newton’ second equation of motion is given by, $v = u + at$ where $v$ is the final velocity of the body, $u$ is its initial velocity, $a$ is the acceleration and $t$ is the time taken.

Complete step by step solution:
Step 1: Sketch a figure depicting the motion of one ball as it leaves the hand of the juggler and list the parameters given.

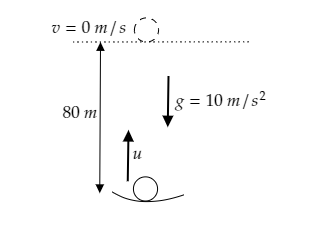
The maximum height reached by the ball will be its displacement and it is given to be $s = 80{\text{m}}$ .
At the maximum height, the final velocity of the ball will be zero i.e., $v = 0$ .
The acceleration of the ball will be the acceleration due to gravity i.e., $a = - g = - 10{\text{m}}{{\text{s}}^{ - 2}}$ .
The number of balls that are being juggled is given to be $n = 10$ .
Let $u$ be the initial velocity of the ball as it starts its ascent and $t$ be the time taken for the ascent of the ball.
Step 2: Using Newton’s third equation of motion, obtain the initial velocity of the ball.
Newton’s third equation of motion for the ascent of one ball can be expressed as ${v^2} = {u^2} - 2gs$ .
$\Rightarrow u = \sqrt {{v^2} + 2gs}$ -------- (1)
Substituting for $v = 0$ , $g = 10{\text{m}}{{\text{s}}^{ - 2}}$ and $s = 80{\text{m}}$ in equation (1) we get, $u = \sqrt {{0^2} + \left( {2 \times 10 \times 80} \right)} = 40{\text{m}}{{\text{s}}^{ - 1}}$
Thus the initial velocity of the ball is obtained to be $u = 40{\text{m}}{{\text{s}}^{ - 1}}$ .
Step 3: Using Newton’s second equation of motion, obtain the time taken for the ascent of the ball.
Newton’ second equation of motion for the ascent of the ball can be expressed as $v = u - gt$ .
$\Rightarrow t = \dfrac{{u - v}}{g}$ ------- (2)
Substituting for $u = 40{\text{m}}{{\text{s}}^{ - 1}}$ , $v = 0$ and $g = 10{\text{m}}{{\text{s}}^{ - 2}}$ in equation (2) we get, $t = \dfrac{{40 - 0}}{{10}} = 4{\text{s}}$
Thus the time for the ascent of the ball is obtained to be $t = 4{\text{s}}$ . The same time is taken for the ball to descend to the juggler’s hand once it reaches maximum height.
So the total time taken for one ball to go up and come down to the juggler’s hand will be ${t_{total}} = 4 + 4 = 8{\text{s}}$ .
Then the time interval maintained to keep all 10 balls at a proper distance will be ${t_{\operatorname{int} erval}} = \dfrac{{{t_{total}}}}{n} = \dfrac{8}{{10}} = 0 \cdot 8{\text{s}}$ .
$\therefore$ the time interval maintained by the juggler is obtained to be ${t_{\operatorname{int} erval}} = 0 \cdot 8{\text{s}}$ .

So the correct option is B.

Note: As the ball reaches the maximum height, its velocity will decrease and drop to zero. However, during the descent of the ball from the maximum height, the velocity of the ball will increase and as it reaches the hand of the juggler, the velocity will be equal to its initial velocity. All the measurements in the upward direction are taken to be positive. Since acceleration due to gravity is directed downwards, we have $a = - g$ .