Question

A jet of water with a cross section of $6\,c{m^2}$ strikes a wall at an angle of $60^\circ$to the normal and rebounds elastically from the wall without losing energy. If the velocity of the water in the jet is 12 m/s, the force acting on the wall is
A. 0.864 N
B. 86.4 N
C. 72 N
D. 7.2 N

Answer 1

We know that rate of change of linear momentum with time is the force. Consider a differential length element of the jet and differential mass to determine the momentum. In the direction of normal force, only the horizontal component of the momentum changes.

Formula used:
$P = mv$
Here, P is the linear momentum, m is the mass and v is the velocity.
The relation between mass, volume and density is,
$\rho = \dfrac{m}{V}$

Complete step by step answer:
We know that the force acting on the body is equal to change in linear momentum of the body with respect to time.
$F = \dfrac{{dP}}{{dt}}$
We also know that the linear momentum of the body is equal to product of mass m and velocity v is,
$P = mv$
We need to find the change in linear momentum of the jet of water. Therefore, we consider the differential length element of the incident jet of the water as $dl$. So, we get the corresponding volume of the small length element,
$dV = a\,dl$
Here, $a$ is the area of cross-section of the differential element.
Also, we can write the differential mass of the differential element as,
$dm = \rho dV$
$\Rightarrow dm = \rho a\,dl$
We have, momentum of this differential element is,
$dp = dm\,v$
$\Rightarrow dp = \left( {\rho a\,dl} \right)v$
$\Rightarrow dp = \rho a\,vdl$
The normal force on the wall due to jet of the water is due to only horizontal component of the linear momentum of differential element as shown in the figure below,

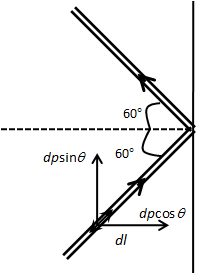
From the above figure, we get the horizontal component of linear momentum of the differential element for incident jet stream is, $dp\cos \theta$.
Therefore,
$d{p_{x,i}} = \rho avdl\cos \theta$
The horizontal component of linear momentum of the differential element for the reflected jet stream is, $- dp\cos \theta$.
Therefore,
$d{p_{x,r}} = - \rho avdl\cos \theta$
Now, the change in linear momentum of the differential element is,
$d{p_x} = - \rho avdl\cos \theta - \rho avdl\cos \theta$
$\Rightarrow \left| {d{p_x}} \right| = 2\rho avdl\cos \theta$
We know that the normal force acting on the wall is the rate of change of the horizontal component of linear momentum of the differential element. Therefore,
$F = \dfrac{{2\rho avdl\cos \theta }}{{dt}}$
$\Rightarrow F = 2\rho av\cos \theta \dfrac{{dl}}{{dt}}$
$\Rightarrow F = 2\rho a{v^2}\cos \theta$
We can substitute $1000\,kg/{m^3}$ for $\rho$, $6 \times {10^{ - 4}}\,{m^2}$ for a, 12 m/s for v and $60^\circ$ for $\theta$ in the above equation.
$F = 2\left( {1000} \right)\left( {6 \times {{10}^{ - 4}}} \right){\left( {12} \right)^2}\cos \left( {60^\circ } \right)$
$\Rightarrow F = 86.4\,N$

So, the correct answer is “Option B”.

Note:
The horizontal component of momentum for incident jets is towards right, therefore, we have taken it as positive while the horizontal component of momentum for reflected jets is towards left. Therefore, we have taken it as negative. The rate of change of length $\dfrac{{dl}}{{dt}}$ is the velocity of the jet stream.