Question

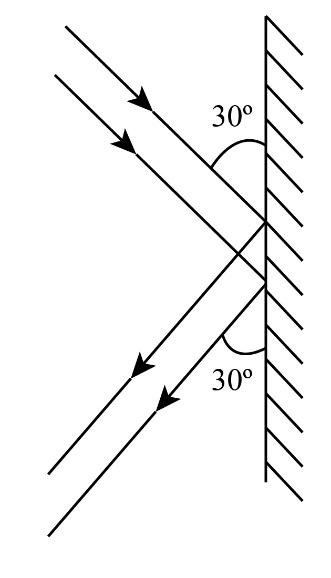
A jet of water $\left( {5{\rm{ kg }}{{\rm{s}}^{ - 1}}} \right)$ travelling with a velocity of $5{\rm{ m}}{{\rm{s}}^{ - 1}}$ makes an angle of $30^\circ$ with the vertical wall as shown in the figure. The jet rebounds with the same speed making an angle of $30^\circ$ with the wall. The average force on the wall is ___________N.

Answer 1

We will use the impulse-momentum equation concept, which gives us the expression for the force exerted by the given jet of water on the vertical wall. The final expression for the force exerted by the water jet is given by the difference of horizontal components of the jet's initial and final velocity.

Complete step by step answer:
The mass flow of a jet of water striking on the vertical wall is $\dot m = 5{\rm{ kg }}{{\rm{s}}^{ - 1}}$.
The velocity of the jet of water is $V = 5{\rm{ m}}{{\rm{s}}^{ - 1}}$.
The angle made by the jet of water while striking and leaving the wall is ${\theta _1} = 30^\circ$.

Let us consider the horizontal direction as the x-axis and vertical direction as the y-axis. We can resolve the initial and final velocity into horizontal and vertical components. On resolving the velocity, we will find that the vertical component is parallel to the wall, which means it does not affect the jet's force on the wall. Therefore, we can say that only horizontal components of initial and final velocities have their effect on the total force exerted by the jet on the wall.

We can express the horizontal component of initial velocity as below:
${V_1} = V\sin \theta$
Here ${V_1}$ is the horizontal component of the initial velocity of the jet.

We can write the horizontal component of the final velocity of the jet of water as below:
${V_2} = - V\sin \theta$

We can write the expression for the force exerted by the jet of water on the vertical wall as below:
$F = \dot m\left( {{V_1} - {V_2}} \right)$
Here F is the force exerted on the jet.

We will substitute $V\sin \theta$ for ${V_1}$ and $- V\sin \theta$ for ${V_2}$ in the above expression.

F = \dot m\left[ {\left( {V\sin \theta } \right) - \left( { - V\sin \theta } \right)} \right]\\\ = 2\dot mV\sin \theta \end{array}$$ We will substitute $$5{\rm{ kg }}{{\rm{s}}^{ - 1}}$$ for $$\dot m$$, $$5{\rm{ m}}{{\rm{s}}^{ - 1}}$$ for V and $$30^\circ $$ for $$\theta $$ in the above expression. $$\begin{array}{c} F = 2\left( {5{\rm{ kg }}{{\rm{s}}^{ - 1}}} \right)\left( {5{\rm{ m}}{{\rm{s}}^{ - 1}}} \right)\sin 30^\circ \\\ = 25{\rm{ N}} \end{array}$$ **Therefore, the force exerted by the jet of water on the wall is equal to $$25{\rm{ N}}$$.** **Note:** Taking the sign convention for the horizontal component of the jet of water's initial and final velocity into consideration and using the concept of equilibrium, we have written the expression for the force exerted by the jet on the wall.