Question

A jet airplane travelling from east to west at a speed of $500km{h^{ - 1}}$ eject out gases of combustion at a speed of $1500km{h^{ - 1}}$ with respect to the jet plane. What is the velocity of the gases with respect to an observer on the ground?

A) $1000km{h^{ - 1}}$ in the direction west to east.
B) $1000km{h^{ - 1}}$ in the direction east to west.
C) $2000km{h^{ - 1}}$ in the direction west to east.
D) $2000km{h^{ - 1}}$ in the direction east to west.

Answer 1

The question is based on the relative velocity. Relative velocity is the velocity which is taken out with respect to another body; usually the relative velocity is taken out between two moving bodies; the bodies can be in the same or different direction.
The velocity of a body with respect to the velocity of another body is called the relative velocity of the first body with respect to the second.

Complete step by step solution:
Step 1: If ${v_A}$ and ${v_B}$represent the velocities of two bodies $A$ and $B$ respectively at any instant, then, the relative velocity of $A$ with respect to $B$ is represented by ${v_{AB}}$.
$\therefore {v_{AB}} = {v_A} - {v_B}$ ------------------- (1)

Similarly, the relative velocity of B with respect to A is given by,

$\therefore {v_{BA}} = {v_B} - {v_A}$ -------------------- (2)

Step 2:

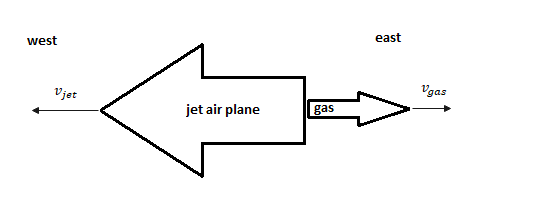
Here, ${v_{jet}} =$ the velocity of the jet plane from east to west with respect to the observer on ground, ${v_{gas}} =$ the speed of the gas with respect to the observer on ground.
Step 3: Therefore from equation (1) the relative velocity of the gas with respect to the jet plane is,

$v = {v_{gas}} - {v_{jet}}$, where $v =$ relative velocity of the gas with respect to the jet plane

According to the question the gases are ejected in the direction opposite to the direction of motion of the plane therefore the relative velocity of the gases with respect to the plane is $- 1500km{h^{ - 1}}$.

$\therefore v = - 1500km{h^{ - 1}}$, ${v_{jet}} = 500km{h^{ - 1}}$
$\therefore v = {v_{gas}} - {v_{jet}}$
$\Rightarrow {v_{gas}} = v + {v_{jet}}$
$\Rightarrow {v_{gas}} = \left( { - 1500 + 500} \right)km{h^{ - 1}}$
$\therefore {v_{gas}} = - 1000km{h^{ - 1}}$

Step 4: $\because {v_{gas}} = - 1000km{h^{ - 1}}$, hence the negative sign indicates that the direction of the velocity of the gas with respect to the observer on ground is from west to east.
Therefore, the velocity of the gases with respect to an observer on the ground is $1000km{h^{ - 1}}$ in the direction west to east.

$\therefore$ The correct option is option (A).

Note: Students must be careful about the direction of the velocity vector when calculating the relative velocity. Also always remember that for relative velocity there should be only one reference frame.