Question
Question: A jar of height h is filled with a transparent liquid of refractive index μ. At the center of the ja...
A jar of height h is filled with a transparent liquid of refractive index μ. At the center of the jar on the bottom surface is a dot. Find the minimum diameter of a disc, such that when it is placed on the top surface symmetrically about the center, dot is invisible.
Solution
To solve this question, we have to apply the rule of total internal reflection. Using the condition for this effect, and applying mathematics on the geometry of the figure, we can get the answer.
Formula used: The formula used in this solution is
⇒iC=sin−1(μ1), here iC is the critical angle of incidence for a light ray travelling from a medium of refractive indexμto the air.
Complete step by step solution:
Let the minimum diameter of the disc be d. The situation is represented in the figure below.
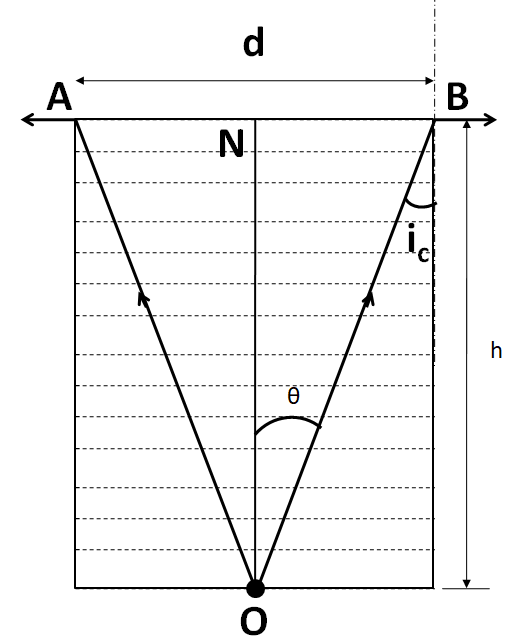
As we can see that the rays are emerging out of the dot at the centre of the jar. The topmost layer of water is an interface, which is separating two mediums, air and water. So the rays emerging out undergo refraction.
For the dot to be invisible outside the jar, none of the rays should come out of the jar. This is only possible when these rays bounce back into the jar, or they slip along the topmost layer of water.
Or in other words, these rays should undergo total internal reflection.
We know that for this effect to take place, the angle of incidence should be greater or equal to the critical angle of incidence iC. For the minimum diameter of the disc, we take it equal to iC.
From the figure we can see that
⇒θ=iC (Alternate interior angles) …………….(i)
As the dot is present at the centre of the jar, so in the above figure
⇒AN=BN=d/2 ………………..(ii)
In triangle BON
⇒sinθ=OBBN ………………..(iii)
By Pythagoras theorem, we have
⇒OB2=BN2+ON2
⇒OB2=(2d)2+h2
Taking under root, we get
⇒OB=4d2+h2
⇒OB=21d2+4h2 …………………….(iv)
Putting (ii) and (iv) in (iii)
⇒sinθ=21d2+4h2d/2
⇒sinθ=d2+4h2d
From (i)
⇒siniC=d2+4h2d …………………..(v)
We know that the critical angle of incidence is given by
⇒iC=sin−1(μ1)
Taking sine both the sides
⇒siniC=μ1 ………………….(vi)
Putting (vi) in (v)
⇒μ1=d2+4h2d
Taking square on both the sides
⇒μ21=d2+4h2d2
On cross multiplying, we get
⇒d2+4h2=μ2d2
Subtractingd2 from both sides
⇒4h2=μ2d2−d2
⇒4h2=d2(μ2−1)
Dividing by (μ2−1)
⇒(1−μ2)4h2=d2
Finally, taking square root on both the sides, we get
⇒d=1−μ22h
Hence, the minimum required diameter of the disc is equal to1−μ22h.
Note:
Before using the effect of total internal reflection, always check its condition. The condition for total internal reflection to take place is that the light ray should be travelling from an optically denser medium to an optically rarer medium. In this question, the light ray from the dot was travelling from water, an optically denser medium to air, an optically rarer medium. So we could make use of this phenomenon.
