Question
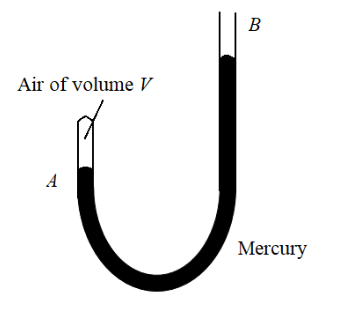
Question: A J-tube shown in the figure contains a volume V of dry air trapped in arm A of the tube. The atmosp...
A J-tube shown in the figure contains a volume V of dry air trapped in arm A of the tube. The atmospheric pressure is H cm of mercury. When more mercury is poured in arm B, the volume of the enclosed air and its pressure undergo a change. What should be the difference in mercury levels in the arms so as to reduce the volume of air to V/2?
(A) Hcm
(B) 2Hcm
(C) 2Hcm
(D) 30Hcm
Solution
Refer to the ideal gas law to determine the pressure at arm A. Use the formula to calculate the pressure below the height h of the liquid column of density ρ.
Complete step by step answer:
According to Ideal gas law, the product of pressure and volume is constant.
Therefore, we can write,
⇒P1V1=P2V2
Here, V1 is the volume of the arm A at atmospheric pressure P1 and V2 is the volume of the arm A at pressure P2.
The initial volume is V and the final volume is 2V. The pressure P1 is the atmospheric pressure P.
Therefore, the above equation becomes,
⇒PV=P22V
⇒p2=2P
We know that the pressure below the height H is,
⇒P=Hρg
Therefore,
⇒p2=2Hρg
Here, ρ is the density of the liquid and g is the acceleration due to gravity.
Let the height of the mercury column is x. The pressure below the height x is the sum of atmospheric pressure and the pressure due to the mercury column above it. We have determined the pressure at the arm A which is 2P.
Therefore,
⇒2P=P0+xρg
We have given, the atmospheric pressure is H cm of mercury. Therefore, the atmospheric pressure is,
⇒P0=Hρg
Therefore, the pressure at arm A is,
⇒2Hρg=Hρg+xρg
⇒2Hρg=ρg(H+x)
⇒2H=(H+x)
⇒∴x=h
So, the correct answer is option (A).
Note: The pressure inside an open liquid column is the addition of atmospheric pressure over the surface of the liquid and the pressure due to liquid above that point.
