Question

'A' is a substance that converts into B, C and D by three first order parallel paths simultaneously according to the following stoichiometry:

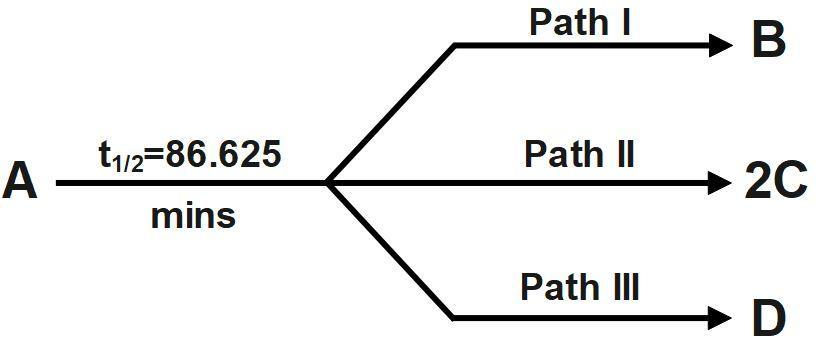
The partial ${{t}_{1/2}}$ of A along path I and path II are $173.25$ min and $346.5$ min respectively. The energies of activation of the reaction along path I, path II and path III are $40,\text{ }60$ and $80\text{ }kJ/mol$ respectively.
1. The percent distribution of C in the product mixture B, C and D at any time is equal to
$20$
$60$
$80$
$40$
2. The initial rate of consumption of A and the sum of the initial rate of formation of B, C and D are respectively, taking $\left[ A \right]=0.25\text{ }M,$ equal to
$2\times {{10}^{-3}}mol{{L}^{-1}}mi{{n}^{-1}}$ and $2.5\times {{10}^{-3}}mol{{L}^{-1}}mi{{n}^{-1}}$
$2\times {{10}^{-3}}mol{{L}^{-1}}mi{{n}^{-1}}$ and $2\times {{10}^{-3}}mol{{L}^{-1}}mi{{n}^{-1}}$
$2.5\times {{10}^{-3}}mol{{L}^{-1}}mi{{n}^{-1}}$ and $3\times {{10}^{-3}}mol{{L}^{-1}}mi{{n}^{-1}}$
$4\times {{10}^{-3}}mol{{L}^{-1}}mi{{n}^{-1}}$ and $2\times {{10}^{-3}}mol{{L}^{-1}}mi{{n}^{-1}}$
3. The overall energy of activation of A along the entire three parallel paths is equal to
(A) $52\text{ }kJ/mol$
(B) $60\text{ }kJ/mol$
(C) $55\text{ }kJ/mol$
(D) $80\text{ }kJ/mol$

Answer 1

Hint : We know that the rate of reaction alludes to the speed at which the products are formed in the reactants in a compound reaction. When we talk about chemical reactions, the rate at which they happen shifts by an incredible arrangement.

Complete Step By Step Answer:
We need to know that according to the overall definition, the speed with which a reaction happens is alluded to as the rate of reaction. For instance, wood burning has a reaction rate that is higher since the process is quick and rusting of iron has a rate of
The reaction is low as the process is moderate. Rate of a chemical reaction depends on the concentrations of reactants or products and the time required to complete the chemical change. Rate of a chemical reaction can be defined as the change in concentration of a reactant or product in unit time. Thus, rate of a chemical reaction can be expressed on the basis of following:
-The rate of decrease in concentration of any one of the reactants or the rate of increase in concentration of any one of the products.
-Time taken in the change in concentration.
The rate of reaction exceptionally relies upon the sort and nature of the reaction. As referenced before, not many reactions are normally quicker than others while a few reactions are very slow. The rate of reaction is for the most part more slow in fluids when contrasted with gases and more slow in solids when contrasted with fluids. Size of the reactant likewise matters a ton. The more modest the size of the reactant, the quicker the reaction.
1. If ${{k}_{1}},\text{ }{{k}_{2}}$ and ${{k}_{3}}$ be the rate constants of the reaction along path I, II and III respectively, then overall rate constant of consumption of A will be ${{k}_{1}}+{{k}_{2}}+{{k}_{3}}.$ So,
$86.625\min =\dfrac{0.693}{{{k}_{1}}+{{k}_{2}}+{{k}_{3}}}$
On further solving we get;
${{k}_{1}}+{{k}_{2}}+{{k}_{3}}=\dfrac{0.693}{86.625\min }=8\times {{10}^{-3}}{{\min }^{-1}}$
Thus, ${{k}_{1}}=\dfrac{0.693}{173.25}=4\times {{10}^{-3}}{{\min }^{-1}}$ and ${{k}_{3}}=8\times {{10}^{-3}}-(4+2)\times {{10}^{-3}}=2\times {{10}^{-3}}{{\min }^{-3}}$
$\therefore \text{ }$
On substituting the values we get-
\text{ % Distribution}of\text{ }C=\dfrac{2\times 2\times {{10}^{-3}}}{10\times {{10}^{-3}}}
On further solving we get-
\Rightarrow\text{% Distribution }of\text{ }C=40

2. As we know that $\dfrac{-d[A]}{dt}=\left( {{k}_{1}}+{{k}_{2}}+{{k}_{3}} \right)[A]$
On substituting the values we get;
$\Rightarrow \dfrac{-d[A]}{dt}=\left( 8\times {{10}^{-3}} \right)\left[ 0.25 \right]=2\times {{10}^{-3}}mol{{L}^{-1}}{{\min }^{-1}}$
Thus, we get here is; $\dfrac{d\left[ B \right]}{dt}+\dfrac{d\left[ C \right]}{dt}+\dfrac{d\left[ D \right]}{dt}={{k}_{1}}\left[ A \right]+2{{k}_{2}}\left[ A \right]+{{k}_{3}}\left[ A \right]$
On further solving we get;
$\left( {{k}_{1}}+2{{k}_{2}}+{{k}_{3}} \right)\left[ A \right]=10\times {{10}^{-3}}\times 0.25$
$\Rightarrow \left( {{k}_{1}}+2{{k}_{2}}+{{k}_{3}} \right)\left[ A \right]=2.5\times {{10}^{-3}}mol{{L}^{-1}}{{\min }^{-1}}$

3. ${{E}_{a(overall)}}=\dfrac{{{k}_{1}}{{E}_{a1}}}{{{k}_{1}}+{{k}_{2}}+{{k}_{3}}}+\dfrac{{{k}_{2}}{{E}_{a2}}}{{{k}_{1}}+{{k}_{2}}+{{k}_{3}}}+\dfrac{{{k}_{3}}{{E}_{a3}}}{{{k}_{1}}+{{k}_{2}}+{{k}_{3}}}$
On further solving we get;
${{E}_{a(overall)}}=0.5\times 40+0.25\times 60+0.25\times 80$
$\Rightarrow {{E}_{a(overall)}}=55~~~kJ/mol$
Therefore, the correct answer is option D, A and C respectively.

Note :
Remember that the higher Temperature also increases the rate of the reaction. The reaction rate is highly affected by the solvent properties and ionic strength. When a catalyst is present, the speed of the reaction raises the reaction speed. Rate of the reaction is also affected by the surface area of the reactants. If the surface area is more, the speed of the heterogeneous chemical reactions increases. Some chemical reactions are almost momentary, while others take some time to attain the final equilibrium.