Question
Question: A' is a huge planet with uniform mass distribution, mass M, radius R. B is a circular tunnel made in...
A' is a huge planet with uniform mass distribution, mass M, radius R. B is a circular tunnel made in it, concentric with planet. Radius of tunnel is r,(r=2R) cross sectional diameter is d (d << r). C is a small ball of mass m (m <<M) which is moving freely inside the tunnel without friction in a uniform circular motion, take acceleration due to gravity on surface of A as g:
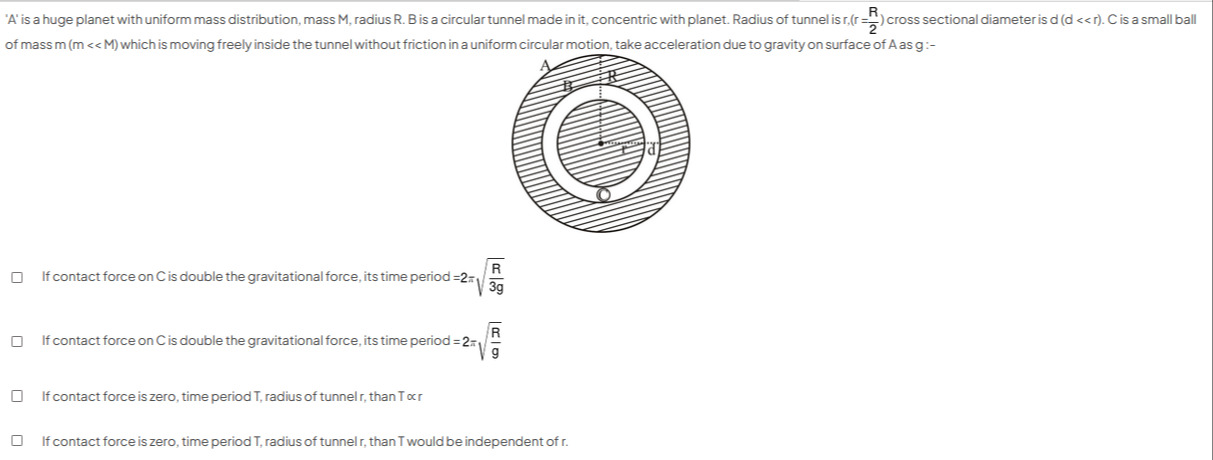
If contact force on C is double the gravitational force, its time period =2π3gR
If contact force on C is double the gravitational force, its time period =2πgR
If contact force is zero, time period T, radius of tunnel r, than T∝r
If contact force is zero, time period T, radius of tunnel r, than T would be independent of r.
If contact force on C is double the gravitational force, its time period =2π3gR
Solution
The gravitational force on the ball C at a distance r from the center of the planet is given by Fg=R3GMmr. We are given that the acceleration due to gravity on the surface of the planet is g=R2GM. So, GM=gR2.
The gravitational force can be written as Fg=R3gR2mr=Rmgr.
In this problem, the radius of the tunnel is r=2R.
So, the gravitational force on the ball is Fg=Rmg(R/2)=2mg. This force is directed towards the center of the planet.
The ball C is moving in a uniform circular motion inside the tunnel of radius r, concentric with the planet. The center of the circular motion is the center of the planet O. The radius of the circular motion is r. For uniform circular motion with speed v, the centripetal force required is Fc=rmv2, directed towards the center O.
The forces acting on the ball are the gravitational force Fg towards O and the contact force N from the tunnel wall. Since the ball is moving in a circular path of radius r around O, the contact force N must be radial. Let's assume the contact force N is positive when directed inwards.
The net force towards the center O is the sum of the gravitational force and the contact force (with appropriate sign).
Net force towards O = Fg+N=rmv2.
Here, Fg is always towards O. If N is inwards, it is positive. If N is outwards, it is negative.
Consider the first option: If contact force on C is double the gravitational force, its time period =2π3gR.
Let N=2Fg. For the net force to be towards the center, the contact force must be directed inwards.
Net force towards O = Fg+N=Fg+2Fg=3Fg.
So, 3Fg=rmv2.
3(2mg)=rmv2.
23mg=rmv2.
v2=23gr.
The time period of uniform circular motion is T=v2πr.
T2=v24π2r2=(3gr/2)4π2r2=3g8π2r.
T=2π3g2r.
We are given r=2R. Substitute this into the expression for T:
T=2π3g2(R/2)=2π3gR.
This matches the first option.
Let's check the other options.
Option 2: If contact force on C is double the gravitational force, its time period =2πgR.
Our calculated time period is 2π3gR. So, option 2 is incorrect.
Option 3: If contact force is zero, time period T, radius of tunnel r, than T∝r.
If contact force N = 0, then the net force towards O is Fg.
Fg=rmv2.
2mg=rmv2.
v2=2gr.
The time period T=v2πr=gr/22πr=2πrgr2=2πgr4π2r2⋅2=2πg2r.
So, T=2πg2r.
This shows that T∝r. Option 3 states T∝r, which is incorrect.
Option 4: If contact force is zero, time period T, radius of tunnel r, than T would be independent of r.
From the calculation in option 3, T=2πg2r, which clearly depends on r. So, option 4 is incorrect.
Therefore, only the first option is correct.
