Question
Question: (a) In Young’s double slit experiment, derive the condition for (i) constructive interference and ...
(a) In Young’s double slit experiment, derive the condition for
(i) constructive interference and
(ii) destructive interference at a point on the screen.
(b) A beam of light consisting of two wavelengths, 800 nm and 600 nm is used to obtain the interference fringes in a Young’s double slit experiment on a screen placed 1.4 m away. If the two slits are separated by 0.28 mm, calculate the least distance from the central bright maximum where the bright fringes of the two wavelengths coincide.
Solution
Hint: We can find the conditions for constructive and destructive interference by considering two coherent sources of light passing through the two slits and forming fringes on a screen placed at some distance from the slits. We will find the path difference of the two wavelengths of lights and will then find that at what intervals from the central maxima, the constructive or destructive interference will occur.
Later in the second part of the problem, we can use the condition obtained for constructive interference to find the location where the bright fringes of given two wavelengths of light coincides.
Complete step-by-step answer:
(a) let us consider S1 and S2 be two narrow slits placed perpendicular to the plane of a paper and a screen is placed on the perpendicular bisector of S1S2, which is illuminated by monochromatic light.
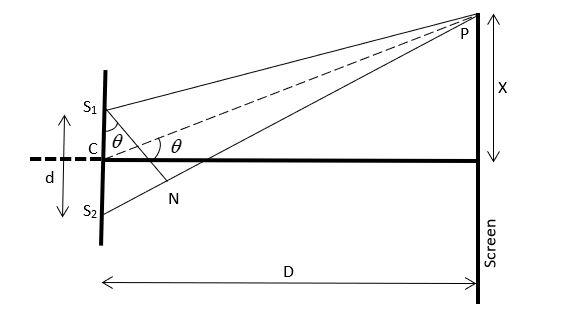
The slits have been placed d distance apart and a screen at a distance D from the slits.
Now, we have a point P on the screen at x distance away from point O on the screen.
Now, the path difference at P between the waves reaching from S1 and S2 is δx=S2P−S1P.
Now, we will draw a perpendicular S1N on S2P
Therefore, δx=S2P−S1P=S2P−NP=S2N
Now, from the triangle S1S2N, we can write that sinθ=S2S1S2N
Therefore, δx=S2N=S2S1sinθ=dsinθ
Since, hereθ is so small, we can write sinθ≃θ=tanθ=Dx
Thus, path difference δx=Dxd
(i) Now, we can find the condition for constructive interference as
Dxd=nλ;n=0,1,2.....
Thus, the position of nth bright fringe, Xn=dnDλ, where n=0 and Xn=0, central bright fringe will be formed at O.
(ii) The condition for destructive interference can be given by
Dxd=(2n−1)2λ, for n = 1, 2…..
(b) We have been given two wavelengths of light λ1 and λ2 with values 800 nm and 600 nm respectively. The distance between slits and the screen, D = 1.4 m and distance between slits, d = 0.28 mm.
We need to find out the least distance of the point on the screen where the bright fringes of two wavelengths of light coincide with each other.
So, let us consider the n1th fringe of wavelength λ1 coincides with the n2th fringe of wavelength λ2.
So, we can write that dn1λ1D=dn2λ2D
⟹n1λ1=n2λ2⟹n2n1=λ1λ2=800600=43
Thus, third bright fringe of light of wavelength n1 will coincide with the fourth bright fringe of light of wavelength n2
So, now least distance of the bright fringe from central bright maxima =d3×λ1D=0.28×10−33×800×10−9×1.4=12mm
Hence the least distance from the central bright maxima, where the two light wavelengths bright fringe will coincide is 12mm.
Note: One more method, we can use to derive the conditions for constructive and destructive interferences by using the wave equations for the two light sources and finding the phase difference or the path difference.
In the second part of the question we can use both the wavelengths to find the distance required but the condition is to find the distance of that bright fringe only respective to that wavelength as which number bright fringe will coincide in case of both wavelengths will be different.
