Solveeit Logo
Login

Question

Question: If $y_1(x)=x$ is a solution of differential equation, then find the other solution $y_2(x)$ and henc...

If y1(x)=xy_1(x)=x is a solution of differential equation, then find the other solution y2(x)y_2(x) and hence the general solution.

(1−x2)d2ydx2+2xdydx+2y=0(1-x^2)\frac{d^2y}{dx^2}+2x\frac{dy}{dx}+2y=0

A

Another solution is y2(x)=−1−x2y_2(x) = -1-x^2. The general solution is y(x)=c1x+c2(−1−x2)y(x) = c_1 x + c_2 (-1-x^2).

B

Another solution is y2(x)=1+x2y_2(x) = 1+x^2. The general solution is y(x)=c1x+c2(1+x2)y(x) = c_1 x + c_2 (1+x^2).

C

Another solution is y2(x)=−1+x2y_2(x) = -1+x^2. The general solution is y(x)=c1x+c2(−1+x2)y(x) = c_1 x + c_2 (-1+x^2).

D

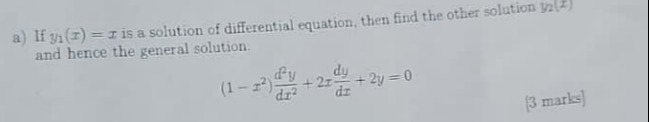
Another solution is y2(x)=x2y_2(x) = x^2. The general solution is y(x)=c1x+c2x2y(x) = c_1 x + c_2 x^2.

Answer

Another solution is y2(x)=−1−x2y_2(x) = -1-x^2. The general solution is y(x)=c1x+c2(−1−x2)y(x) = c_1 x + c_2 (-1-x^2).

Explanation

Solution

The given differential equation is (1−x2)d2ydx2+2xdydx+2y=0(1-x^2)\frac{d^2y}{dx^2}+2x\frac{dy}{dx}+2y=0. We are given that y1(x)=xy_1(x)=x is a solution. To find another linearly independent solution y2(x)y_2(x), we use the method of reduction of order. The formula for the second solution is: y2(x)=y1(x)∫e−∫p(x)dx[y1(x)]2dxy_2(x) = y_1(x) \int \frac{e^{-\int p(x) dx}}{[y_1(x)]^2} dx

First, rewrite the ODE in standard form d2ydx2+p(x)dydx+q(x)y=0\frac{d^2y}{dx^2} + p(x)\frac{dy}{dx} + q(x)y = 0 by dividing by (1−x2)(1-x^2): d2ydx2+2x1−x2dydx+21−x2y=0\frac{d^2y}{dx^2} + \frac{2x}{1-x^2}\frac{dy}{dx} + \frac{2}{1-x^2}y = 0 Here, p(x)=2x1−x2p(x) = \frac{2x}{1-x^2}.

Next, calculate the integral of p(x)p(x): ∫p(x)dx=∫2x1−x2dx\int p(x) dx = \int \frac{2x}{1-x^2} dx Let u=1−x2u = 1-x^2, so du=−2xdxdu = -2x dx. ∫2x1−x2dx=∫−duu=−ln⁡∣u∣=−ln⁡∣1−x2∣\int \frac{2x}{1-x^2} dx = \int \frac{-du}{u} = -\ln|u| = -\ln|1-x^2|.

Now, calculate e−∫p(x)dxe^{-\int p(x) dx}: e−∫p(x)dx=e−(−ln⁡∣1−x2∣)=eln⁡∣1−x2∣=∣1−x2∣e^{-\int p(x) dx} = e^{-(-\ln|1-x^2|)} = e^{\ln|1-x^2|} = |1-x^2|. Assuming we are working in an interval where 1−x2>01-x^2 > 0 (e.g., ∣x∣<1|x|<1), we can write this as 1−x21-x^2.

Substitute y1(x)=xy_1(x)=x and e−∫p(x)dx=1−x2e^{-\int p(x) dx} = 1-x^2 into the formula for y2(x)y_2(x): y2(x)=x∫1−x2x2dxy_2(x) = x \int \frac{1-x^2}{x^2} dx y2(x)=x∫(1x2−1)dxy_2(x) = x \int \left(\frac{1}{x^2} - 1\right) dx y2(x)=x(−1x−x+C)y_2(x) = x \left(-\frac{1}{x} - x + C\right), where CC is the constant of integration. y2(x)=−1−x2+Cxy_2(x) = -1 - x^2 + Cx.

For a linearly independent solution, we take the part of y2(x)y_2(x) that is not proportional to y1(x)y_1(x). The term CxCx is linearly dependent on y1(x)=xy_1(x)=x. Thus, we take the constant part by setting C=0C=0 (or by considering the non-y1y_1 dependent part): y2(x)=−1−x2y_2(x) = -1 - x^2.

The general solution of a second-order linear homogeneous differential equation is given by y(x)=c1y1(x)+c2y2(x)y(x) = c_1 y_1(x) + c_2 y_2(x), where c1c_1 and c2c_2 are arbitrary constants. y(x)=c1x+c2(−1−x2)y(x) = c_1 x + c_2 (-1 - x^2)