Question
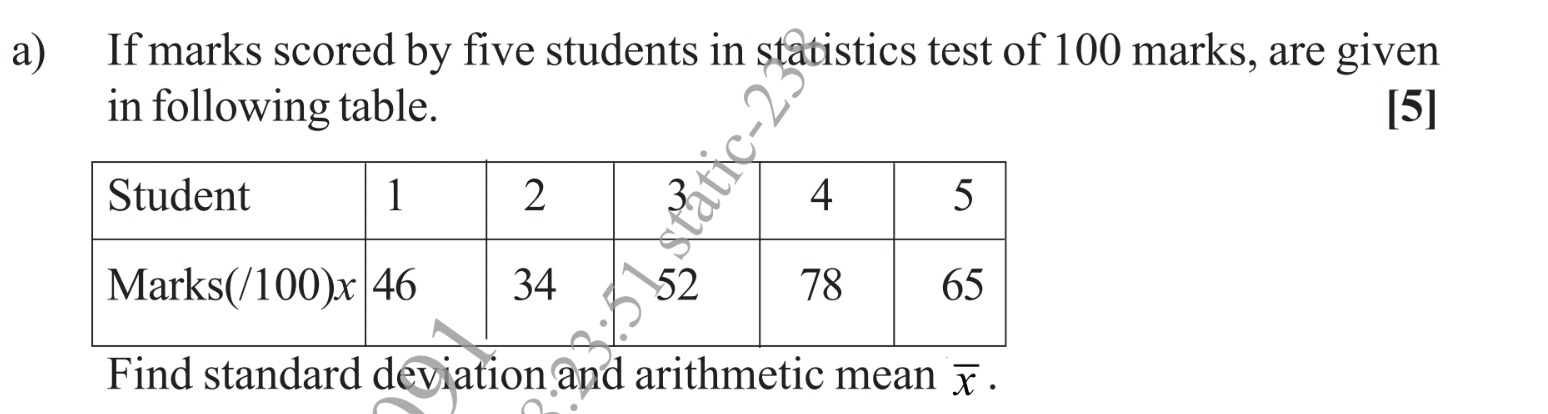
Question: If marks scored by five students in statistics test of 100 marks, are given in following table. | S...
If marks scored by five students in statistics test of 100 marks, are given in following table.
| Student | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Marks(/100)x | 46 | 34 | 52 | 78 | 65 |
Find standard deviation and arithmetic mean x.
Arithmetic mean x=55.
Standard deviation σ=232≈15.23.
Solution
Given the marks of five students in a statistics test: x={46,34,52,78,65}. The number of students is n=5.
First, calculate the arithmetic mean (x). The formula for the arithmetic mean is x=n∑xi. Sum of marks ∑xi=46+34+52+78+65=275. x=5275=55.
Next, calculate the standard deviation (σ). We will use the formula for the population standard deviation, as the given data represents the scores of the specified five students. The formula for the population standard deviation is σ=n∑(xi−x)2. First, calculate the deviations from the mean (xi−x):
46−55=−9
34−55=−21
52−55=−3
78−55=23
65−55=10
Next, square the deviations (xi−x)2:
(−9)2=81
(−21)2=441
(−3)2=9
(23)2=529
(10)2=100
Now, sum the squared deviations ∑(xi−x)2: ∑(xi−x)2=81+441+9+529+100=1160.
Finally, calculate the standard deviation: σ=51160=232. The value of 232 is approximately 15.23.
Explanation of the solution:
- The arithmetic mean x is calculated as the sum of all marks divided by the number of students: x=n∑xi.
- The standard deviation σ is calculated as the square root of the variance, where the variance is the average of the squared deviations from the mean: σ=n∑(xi−x)2.
