Question

A hyperbola having the transverse axis of length $2\sin \theta$, is confocal with the ellipse $3{{x}^{2}}+4{{y}^{2}}=12$, then its equation is ?

Answer 1

In this problem we need to find the equation of the hyperbola which is confocal with the given ellipse and the having the transverse axis length $2\sin \theta$. Now we will consider the equation of the ellipse and convert it into the format $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ to know the values of $a$, $b$. After knowing the value of $a$, $b$ we will calculate the eccentric of the ellipse by using the formula $e=\sqrt{1-\dfrac{{{b}^{2}}}{{{a}^{2}}}}$ after that we will calculate the focus of the ellipse which is given by $\left( \pm ae,0 \right)$. In the problem we have given that the required hyperbola and the given ellipse are the confocal that means the focus of both the shapes is same. So, we will assume the parameter of required hyperbola as $a'$, $b'$, $e'$. From this we have given the length of the transverse axis from this we can calculate the value of $a'$. From the value of $a'$ and focus we can calculate the value of eccentricity of the hyperbola which is given by $e'$. After having the values of $a'$, $e'$ we can calculate the value of $b'$ by using the formula $b{{'}^{2}}=a{{'}^{2}}\left( {{e}^{2}}-1 \right)$. Now we can write the equation of the required hyperbola as $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$.

Complete step by step answer:
Given equation of the ellipse is $3{{x}^{2}}+4{{y}^{2}}=12$.
Dividing the above equation with $12$ on both sides, then we will get
$\begin{aligned} & \dfrac{3{{x}^{2}}+4{{y}^{2}}}{12}=\dfrac{12}{12} \\\ & \Rightarrow \dfrac{3{{x}^{2}}}{12}+\dfrac{4{{y}^{2}}}{12}=1 \\\ & \Rightarrow \dfrac{{{x}^{2}}}{4}+\dfrac{{{y}^{2}}}{3}=1 \\\ \end{aligned}$
Comparing the above equation with $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$, then we will have
${{a}^{2}}=4\Rightarrow a=\pm 2$, ${{b}^{2}}=3\Rightarrow b=\pm \sqrt{3}$.
Now the eccentricity of the ellipse is given by
$\begin{aligned} & e=\sqrt{1-\dfrac{{{b}^{2}}}{{{a}^{2}}}} \\\ & \Rightarrow e=\sqrt{1-\dfrac{3}{4}} \\\ & \Rightarrow e=\sqrt{\dfrac{4-3}{4}} \\\ & \Rightarrow e=\dfrac{1}{2} \\\ \end{aligned}$
Now the focus of the ellipse is given by $\left( \pm ae,0 \right)=\left( \pm 2\times \dfrac{1}{2},0 \right)=\left( \pm 1,0 \right)$.

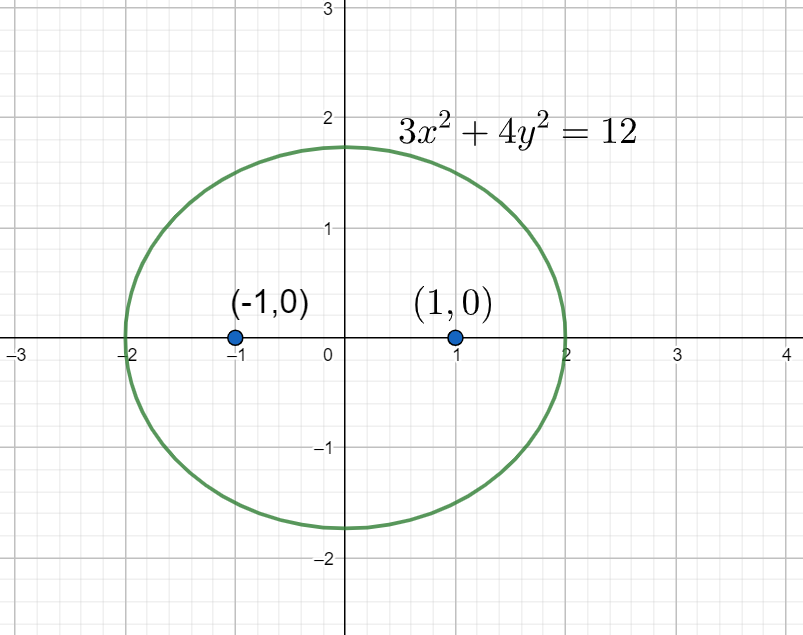
Given the both the required hyperbola and the ellipse are confocal that means the focus of the ellipse and hyperbola are same. So, the focus of the required hyperbola is $\left( \pm 1,0 \right)$.
Let us assume the parameters of the required hyperbola as $a'$, $b'$, $e'$.
Given that the length of traverse axis of the hyperbola is $2\sin \theta$. But the actual length of the traverse axis of the hyperbola is given by
$\begin{aligned} & 2a'=2\sin \theta \\\ & \Rightarrow a'=\sin \theta \\\ \end{aligned}$
We have the focus of the hyperbola as $\left( \pm 1,0 \right)$. But we know that the focus of the hyperbola is $\left( \pm a'e',0 \right)$. Equating the both values, then we will have
$a'e'=1$
Substituting the value $a'=\sin \theta$ in the above equation, then we will get
$\begin{aligned} & \sin \theta \times e'=1 \\\ & \Rightarrow e'=\dfrac{1}{\sin \theta } \\\ \end{aligned}$
Now calculating the value of $b'$ from the formula $b{{'}^{2}}=a{{'}^{2}}\left( {{e}^{2}}-1 \right)$, then we will have
$b{{'}^{2}}={{\left( \sin \theta \right)}^{2}}\left[ {{\left( \dfrac{1}{\sin \theta } \right)}^{2}}-1 \right]$
Simplifying the above equation and using the trigonometric formula $\dfrac{1}{\sin \theta }=\csc \theta$, then we will get
$b{{'}^{2}}={{\sin }^{2}}\theta \left( {{\csc }^{2}}\theta -1 \right)$
From the trigonometric identity ${{\csc }^{2}}\theta -{{\cot }^{2}}\theta =1$, we can write the value of ${{\csc }^{2}}\theta -1$ as ${{\cot }^{2}}\theta$. Substituting this value in the above equation, then we will have
$b{{'}^{2}}={{\sin }^{2}}\theta \times {{\cot }^{2}}\theta$
Substituting the trigonometric formula $\cot \theta =\dfrac{\cos \theta }{\sin \theta }$ in the above equation, then we will get
$\begin{aligned} & b{{'}^{2}}={{\sin }^{2}}\theta \times \dfrac{{{\cos }^{2}}\theta }{{{\sin }^{2}}\theta } \\\ & \Rightarrow b{{'}^{2}}={{\cos }^{2}}\theta \\\ & \Rightarrow b'=\cos \theta \\\ \end{aligned}$
Now the equation of the hyperbola is given by
$\begin{aligned} & \dfrac{{{x}^{2}}}{a{{'}^{2}}}-\dfrac{{{y}^{2}}}{b{{'}^{2}}}=1 \\\ & \Rightarrow \dfrac{{{x}^{2}}}{{{\sin }^{2}}\theta }-\dfrac{{{y}^{2}}}{{{\cos }^{2}}\theta }=1 \\\ \end{aligned}$
Hence the equation of the required hyperbola is $\dfrac{{{x}^{2}}}{{{\sin }^{2}}\theta }-\dfrac{{{y}^{2}}}{{{\cos }^{2}}\theta }=1$.

Note: In this problem they have mentioned that both the required hyperbola and the ellipse are confocal so we have taken the focus of both the shapes as equal. Sometimes they may give that both are concentric then we will take the eccentricity of both the shapes as equal.