Question

A hydraulic press has a ram of 15 cm diameter and a plunger is 1.5 cm. It is required to lift a weight of 1 tonne. The force required on the plunger is
A. 10 kg
B. 100 kg
C. 1000 kg
D. 1 kg

Answer 1

Hydraulic press is an application of Pascal's law following the principle that "The pressure exerted at any point on an enclosed liquid gets transmitted equally in all directions". Also, 1 tonne is measured to be 1000 kilograms.

Formula used:
From the fact that pressure at all points is same, we get:
$F_1 = \dfrac{A_1}{A_2} \times F_2$

Complete step-by-step solution:
In a hydraulic press when we apply pressure on one end, it gets distributed and pressure everywhere in the liquid becomes the same. Pressure is nothing but force per unit area:
$P = \dfrac{force}{area}$

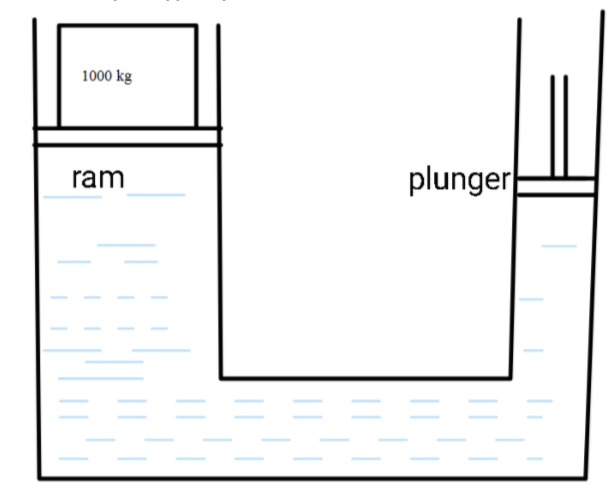
The hydraulic press consists of a tube filled with liquid. Therefore in a hydraulic press towards the ram side, replace the object to be lifted and this side has a bigger area ($A_2$) and on the plunger side, the tube has a smaller area ($A_1$). The ratio of applied force to the area of that side remains equal. Therefore, towards the plunger side, the denominator is small, which requires a small numerator to keep the balance. Towards the ram side, the area is more so Force in the numerator has to be more. When we apply a small force towards the plunger side (downwards), the object placed on the ram side experiences a greater force upwards and gets lifted.
Equating the pressures on two sides:
$\dfrac{F_2}{A_2} = \dfrac{F_1}{A_1}$
We are given:
$R_1 = 1.5$cm
$R_2 = 15$cm
$F_2 = 1000 kg$
Keeping the values we get:
$\dfrac{1000}{\pi (15)^2} = \dfrac{F_1}{\pi (1.5)^2}$
Which gives us
$F_1 = 10 kg$
Therefore, the correct answer is option (A) 10 kg.

Note: Here we expressed force in terms of unit of mass. Here we can do so because the g on both sides will get cancelled automatically so we need not bother about it as it will not affect our result anyway. Also so we did not bother to convert centimeters into meters as the unit gets cancelled anyway. But it is advisable to check the unit system first and make unit conversions and then solve the question in any other circumstance.