Question
Question: A hunter aims at a monkey sitting on a tree at a considerable distance. At an instant he fires at it...
A hunter aims at a monkey sitting on a tree at a considerable distance. At an instant he fires at it, the monkey drops. Will the bullet hit the monkey?
(A) no
(B) Yes
(C) Sometimes
(D) Never
Solution
When an object is projected upwards with some initial velocity and angle less than 90 degree it follows a parabolic path. This type of motion is called projectile motion. In projectile motion only gravitational acceleration acts on the object.
Formula used:
(i) v=u+at
(ii)v2=u2+2as
(iii)s=ut+21at2
Where, u represents the initial velocity, t is the time, v is the final velocity and s denotes the distance.
Complete step by step answer:
Yes, the bullet will hit the monkey. As at the same instant when the hunter fires the bullet, the monkey also drops. Now both, bullet and monkey will experience the same downward acceleration due to gravity ‘g’. Therefore, it will lower the height of both bullet and money, by the same amount. Following is the figure showing the situation.
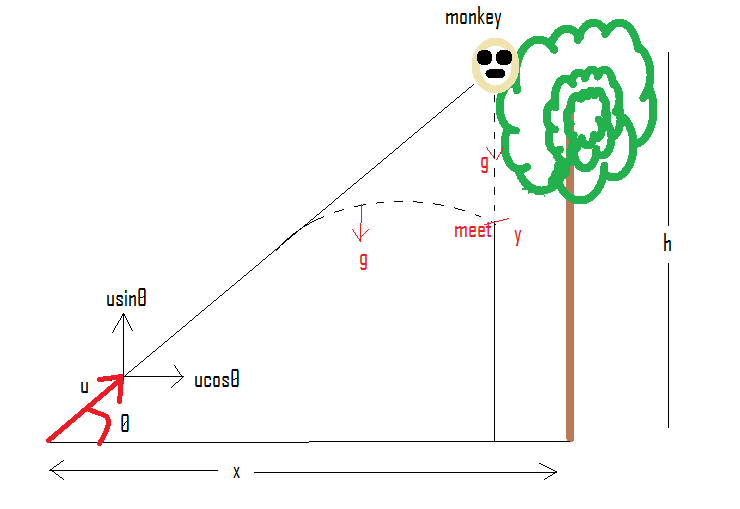
Suppose a bullet is fired with initial velocity u and its distance from tree is x. it will follow projectile motion, so we can break it into its x and y component. The x or horizontal component of velocity will be constant and the vertical component will be decreased by the acceleration due to gravity.
Monkeys will fall with initial velocity u = 0 and will also suffer acceleration due to gravity.
Let both the bullet and monkey meet at point y in time t.
Let us first find the expression for distance and time for monkeys.
Let us use the formulas=ut+21at2
We have the following values for monkeys.
s=y−h,u=0,a=−g
Let us now substitute the values in the above equation.
y−h=−21gt2
Let us further simplify it.
y=h−21gt2 (1)
Now, let us find the expression for a bullet.
For horizontal motion:
s=x,ux=ucosθ,a=0
Let us substitute these values in the equation below.
s=ut+21at2
x=ucosθt (2)
For vertical motion:
s=y,uy=usinθ,a=−g
Let us substitute these values in the equation below.
s=ut+21at2
y=usinθt−21gt2
Substituting the value of “t” from equation (2).
y=usinθ(ucosθx)−21gt2
Let us further simplify it.
y=xtanθ−21gt2 (3)
Now, our aim is to make equation (1) and (3) similar to show that the bullet will hit the monkey.
Let us use the following figure to find the value of tan θ.
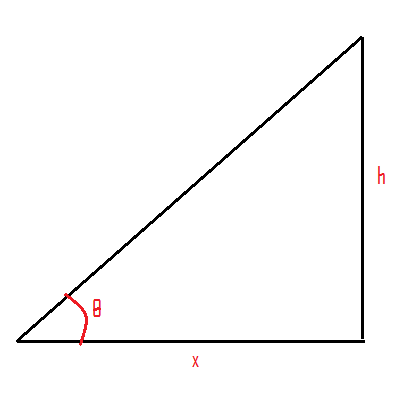
tanθ=xh⇒h=xtanθ
Let us substitute this value of h in equation (3).
y=xtanθ−21gt2 (4)
Hence, equation (1) for monkeys is similar to equation (4) for the bullet. Hence, the bullet will hit the monkey at point y.
Additional information:
We can define acceleration as the rate of change of velocity with respect to time. It has both magnitude and direction; hence it is a Vector quantity. The dimensional formula for the acceleration is L T-2.
The understandings of accelerations are due to Galileo Galilei and Isaac Newton. When objects free fall in vacuum without any drag they experience gravitational acceleration.
We represent the acceleration due to gravity at the surface of the earth by the letter ‘g’ and the standard value is 9.8 m/s2
Note:
If the monkey will not drop at the same instant when the bullet is fired, the bullet will not hit the monkey.
Besides that to calculate precisely, we need to know the velocity of the bullet, angle of projection and height of the tree.
