Question

A housewife wishes to mix together two kinds of food, I and II, in such a way that the mixture contains at least 10 units of vitamin A, 12 units of vitamin B and 8 units of units of vitamin C. The content of vitamins per kg of the foods is shown below

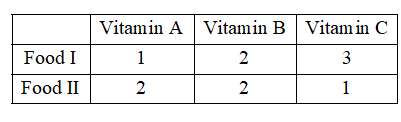
1 Kg of food I costs Rs 6 and 1 kg of food II costs Rs 10. Formulate the above problem as a linear programming problem and find the least cost of the mixture which will produce the diet.

Answer 1

Assume that the amount of Food I used be x and the amount of Food II be y. Hence form the constraint that the total vitamin A content of the mixture should be at least 10. Similarly form the constraint that the total Vitamin B content of the mixture should be at least 12 and the constraint that the total vitamin C content should be at least 8 units. Form the objective function describing the total cost of the mixture. Hence form the LPP with the objective to minimize the objective function.
Hence find the optimal cost of the mixture

Complete step-by-step answer:
Let the amount of Food I used be x kgs and the amount of Food II used be y kgs.
Since the total vitamin A content of the mixture should be at least 10 units and the vitamin A content of Food I is 1 units per kg and the vitamin content of Food II is 2 units per kg, we have
$x+2y\ge 10$
Similarly, since the total vitamin B content of the mixture should be at least 12 units, we have
$2x+2y\ge 12$
Dividing both sides by 2, we get
$x+y\ge 6$
Also, since the total vitamin C content of the mixture should be at least 8 units, we have
$3x+y\ge 8$
Also, since the amount of the foods is non-negative, we have
$x\ge 0,y\ge 0$
Also, the cost of the mixture is given by $Z=6x+10y$
Hence our Linear programming problem is
Minimize:
$Z=6x+10y$
Subject to the constraints
$\begin{aligned} & x+2y\ge 10 \\\ & x+y\ge 6 \\\ & 3x+y\ge 8 \\\ & x\ge 0,y\ge 0 \\\ \end{aligned}$
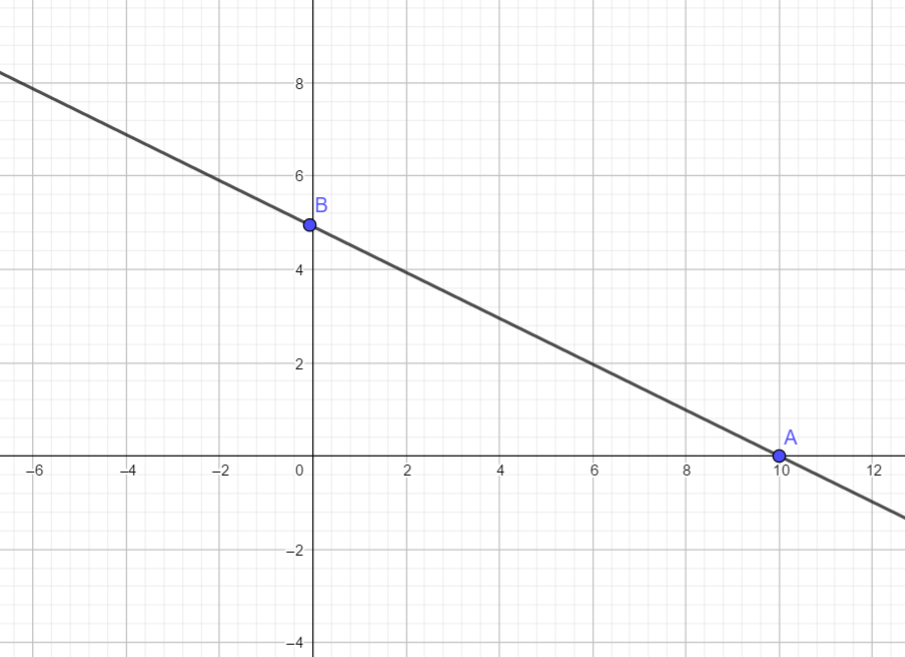
We plot the lines x+2y = 10, x+y = 6 and 3x+y = 8 and locate the feasible region.
For the line x+2y = 10
When x = 0, we have
2y = 10
Dividing both sides by 2, we get
y = 5
When y = 0, we have
x =10
Hence the two points on the line are
A(10,0) and B(0,5)
Plotting these points on the graph paper and joining AB, we get the following graph

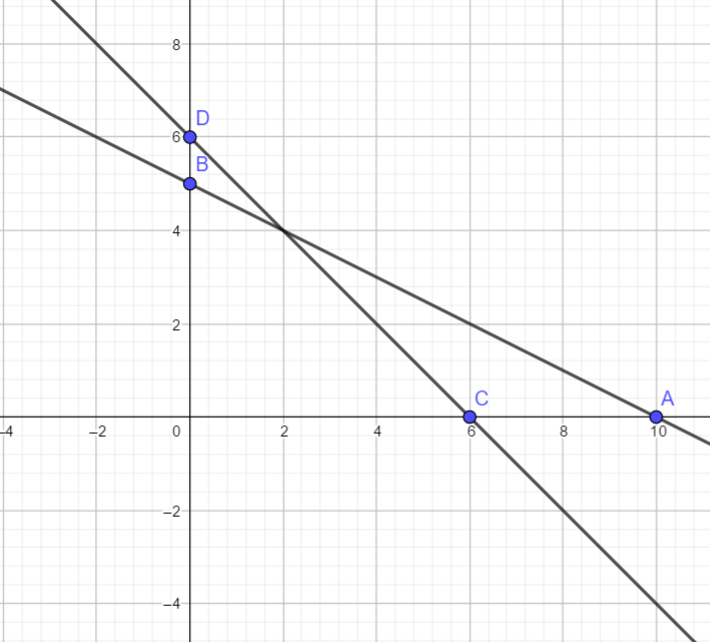
Similarly, for the line x+y = 6, we have when x = 0, y = 6 and when y = 0, x = 6.
Hence the points on the line are C(6,0) and D(0,6)
Plotting this line on the same graph paper, we get the following graph

And for the line 3x+y = 8, we have when y = 5, x= 1 and when x = 0, y = 8.
Hence the points on the line are E(1,5) and F(0,8)
Plotting these points on the above graph and joining EF, we get the following graph

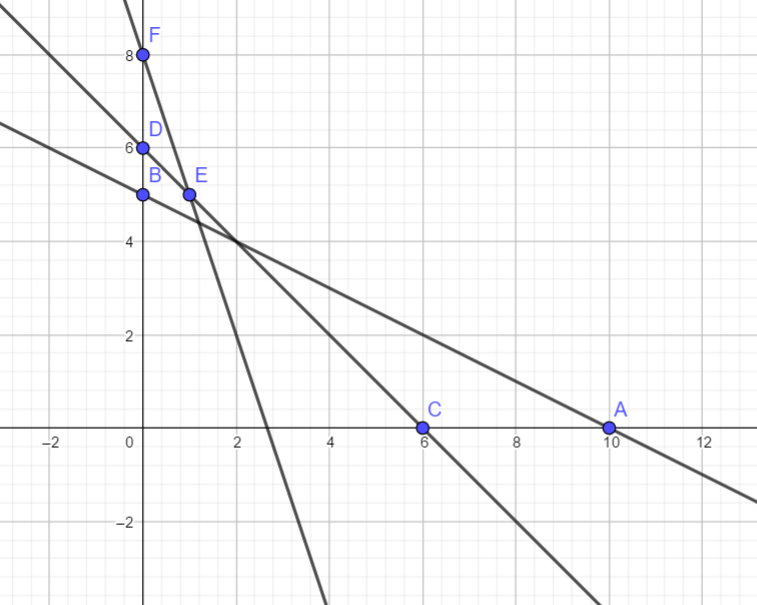
Hence the feasible region is shown shaded below

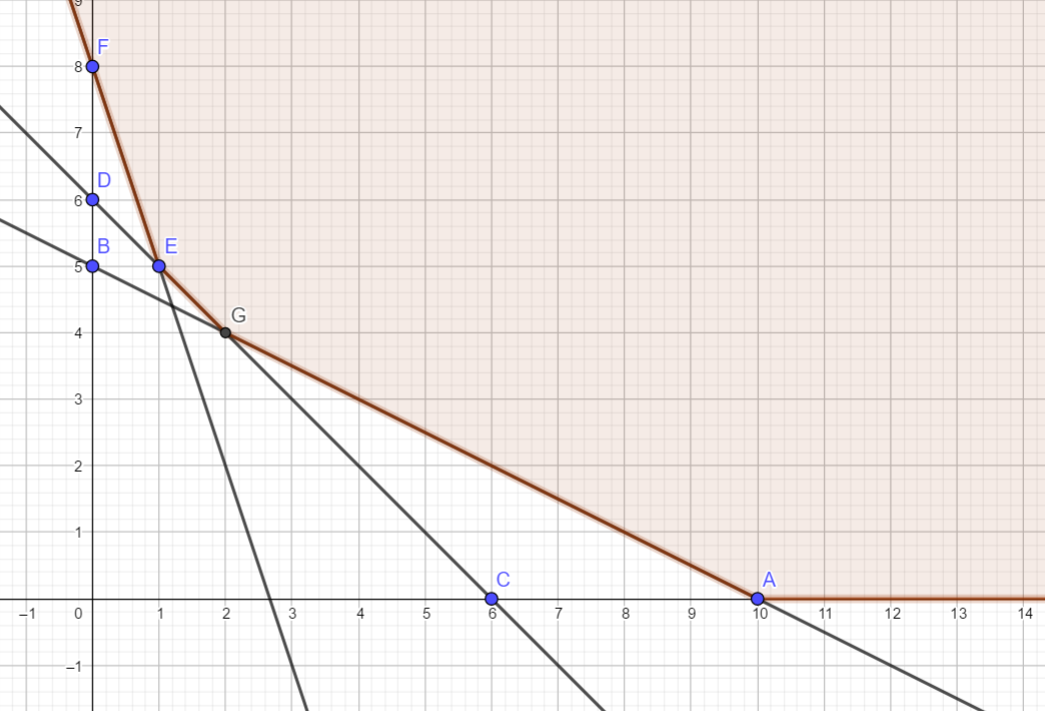
Hence the feasible region is unbounded above and lower bounded by FEGA
Finding coordinates of G.
G is the point of intersection of the line x+2y = 10 (i) with x+y = 6 (ii)
Subtracting equation (i) and (ii), we get
y = 4
Substituting the value of y in equation (ii), we get
x=6-4 = 2
Hence, we have
$G\equiv \left( 2,4 \right)$
Now since we have to minimize the optimal function if the equation 6x+10y = c moves towards the unbounded region of the feasible region, as c decreases, then the optima will not exist, otherwise the optimal will be at the corner point.
So plotting the lines 6x+10y = 2 and 6x+10y = 10 as shown in the graph below

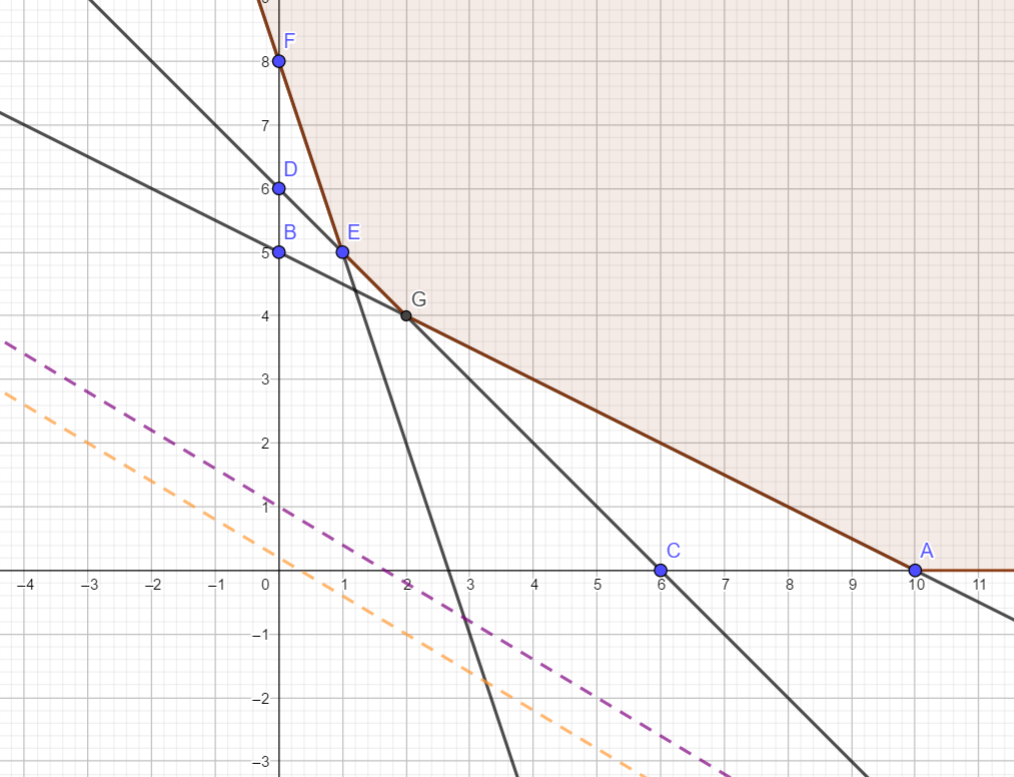
The line 6x+10y =2 is the orange line in the graph and the line 6x+10y = 10 is the purple line in the graph.
As can be seen that as c decreases the line 6x+10y = c moves towards the bounded region of the feasible region.
Hence the optimal value exists.
Checking value at F(0,8)
We have $Z=6\times 0+10\times 8=80$
Checking value at E(1,5)
We have $Z=6\times 1+10\times 5=56$
Checking value at G(2,4)
We have $Z=6\times 2+10\times 4=52$
Checking value at A(10,0) we have
$Z=6\times 10+0=60$
Hence the minima occurs at x = 2 and y = 4 and the minimum value is Rs 52.

Note: Verification:
One should always verify that the values of x and satisfy all the constraints of the LPP.
Constraints $x\ge 0,y\ge 0$ are trivially satisfied.
For the constraint $x+2y\ge 10$, we have $x+2y=2+2\left( 4 \right)=10$
Hence the constraint is satisfied.
For the constraint $x+y\ge 6$, we have $x+y=2+4=6$
Hence the constraint is satisfied.
For the constraint $3x+y\ge 8$, we have
$3x+y=3\left( 2 \right)+4=10\ge 8$
Hence the constraint is satisfied.
Hence all the constraints are satisfied
Hence our solution is correct.