Question

A hose lying on the ground shoots a stream of water upward at an angle of $40^\circ$ to the horizontal. The speed of the water is $20\,m{s^{ - 1}}$ as it leaves the hose. How high up will it strike a wall which is $8\,m$ away?

Answer 1

To solve the question, we must first compute the projectile's initial horizontal and vertical velocity. Then we'll calculate how long it takes the water stream to reach the 8-meter wall. Finally, we'll determine the projectile's vertical location at this point in time.

Complete step by step answer:
The horizontal and vertical components of the water's velocity must first be determined. We achieve this by visualising the velocity as the hypotenuse of a right-angled triangle, with the horizontal and vertical components representing the horizontal and vertical sides.

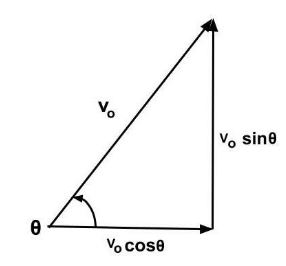
Initial velocity is given as $= {v_0} = 20\,m{s^{ - 1}}$
Horizontal component is given as,
${v_{hor}} = {v_0}\cos \left( \theta \right) \\\ \Rightarrow {v_{hor}} = 20\,m{s^{ - 1}} \times \cos \left( {{{40}^ \circ }} \right) \\\ \Rightarrow {v_{hor}} = 15.3\,m{s^{ - 1}}$
Vertical component is given by,
${v_{vert}} = {v_0}\sin \left( \theta \right) \\\ \Rightarrow {v_{vert}} = 20\,m{s^{ - 1}} \times \sin \left( {{{40}^ \circ }} \right) \\\ \Rightarrow {v_{vert}} = 12.9\,m{s^{ - 1}}$

The next step is to calculate how long it takes the water to reach the wall. The horizontal velocity and the distance to the wall can be used to accomplish this.
$t = \dfrac{d}{v} \\\ \Rightarrow t= \dfrac{{8m}}{{15.3m{s^{ - 1}}}} \\\ \Rightarrow t= 0.522\,s$
We can now employ the kinematics equation.
$s = {v_0}t + \dfrac{1}{2}a{t^2}$
Where: the displacement of the body is denoted by the letter $s$ (basically how high up the water hits the wall). ${v_0}$ is the starting velocity of the body (in this situation, $12.9\,m{s^{ - 1}}$ for the vertical component). $a$ is the body's acceleration (in this case due to gravity; we'll take $9.81\,m{s^{ - 1}}$ ) and $t\left( {0.522{\text{ }}s} \right)$ is the time taken.
$s = 12.9m{s^{ - 1}} \times 0.522s + \dfrac{1}{2} \times 9.81m{s^{ - 1}} \times {\left( {0.522s} \right)^2} \\\ \therefore s = 5.38m \\\$
Therefore, the water reaches the wall $5.38\,m$ above where it started.

Note: This is one of the approaches for answering the question, which is to first calculate the time it takes to reach the horizontal location $x = 8\,m$ and then calculate the vertical position of the projectile at $x = 8m$ . The equation of trajectory of a projectile motion is another simple technique to answer this question. When the other coordinate of a position is known, it is used to find one of the coordinates.