Question

A horizontal tube of length 2 m and initially filled with water is rotated with constant angular velocity $\omega$. Water flows out through a small hole at the other end. Find the velocity of flow of the fluid of density $\rho$ as a function of the length x of the liquid left in the tube?

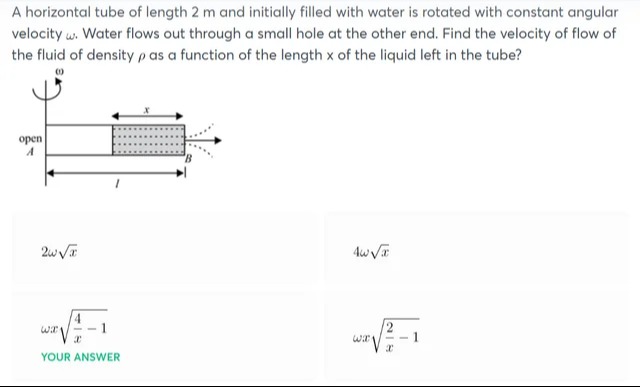
• A. $2\omega\sqrt{x}$
• B. $4\omega\sqrt{x}$
• C. $\omega x \sqrt{\frac{4}{x}-1}$
• D. $\omega x \sqrt{\frac{2}{x}-1}$

Answer 1

Answer: (C)

$\omega x \sqrt{\frac{4}{x}-1}$

Answer 2

The velocity of flow of the fluid as a function of the length x of the liquid left in the tube is given by $\omega x \sqrt{\frac{4}{x}-1}$. This is derived using Bernoulli's equation in a rotating frame of reference, considering the pressure difference and centrifugal force acting on the fluid.