Question

A horizontal plane supports a fixed vertical cylinder of radius R and a particle is attached to the cylinder by a horizontal thread AB as shown in the figure. The particle initially rests on a horizontal plane. A horizontal velocity ${v_0}$ is imparted to the particle, normal to the threading during subsequent motion. Point out the false statements:

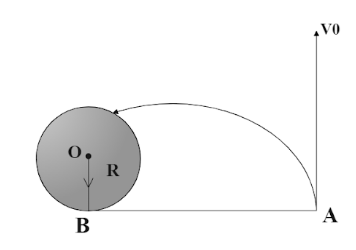
(A) Angular momentum of particle about O remains constant
(B) Angular momentum about B remains constant
(C) Momentum and kinetic energy both remain constant
(D) Kinetic energy remains constant

Answer 1

The change in angular momentum with respect to time on a body is called the torque acting on that body. Also change in velocity is the linear momentum the body possesses. Also, angular momentum is affected by linear momentum for a point particle.

Formula used: We will be using the formulas concerning conservation of force according to the free body diagram. Also we will be using, $\tau = rF\sin \theta$ where $r$ is the radius of the surface on which force is acting, $F$ is the force that acts on the surface, and $\theta$ is the angle between the vector that connects the $F$ and $r$ vector. Also we will be using, $L = rmv\sin \phi$ where $L$ is the angular momentum of a point, $r$ is the radius upon which it acts, $m$ is the mass of the object which causes the momentum, $v$ is the velocity at which the object moves, and $\phi$ is the angle between the radius vector and velocity vector. We might also use the formula $\tau = \dfrac{{dL}}{{dt}}$ where $\tau$ is the torque, $L$ is the angular momentum, and $t$ is the time.

Complete Step by step answer
Observing the free body diagram for the question, we can find which of the forces are conserved in the system.

As you can see, the vertical cylinder is mounted in a horizontal plane (not shown in fig). The cylinder is attached to a particle via thread AB. Thus, it is touching the cylinder at B. Initially the particle is at rest at the position A.
At this position, the particle will experience 3 major forces. The gravitational force that pulls the particle downwards $Fg = mg$ where $Fg$ is the gravitational force, $m$ is the mass of the object, and $g$ is the acceleration due to gravity. Also, a normal force $N$ acts opposite to gravity. Obviously, there is tension $T$ created on the thread AB.
$N = mg$ Thus, these forces are conserved. While tension $T$ is left unbalanced.
Also note that the particle at A is in motion along ${v_0}$ , thus producing a torque $\tau$ at B and also at O (the centre of the circular surface below).
[ Since , $\tau = rmv0\sin \theta$ and none of the variables are zero, there is a torque $\tau$ ]
So now we know for sure that the torque at points B and O, $\tau \ne 0$ .
Also, we know that Torque is also defined as the rate of change of angular momentum.
$\Rightarrow \tau = \dfrac{{dL}}{{dt}}$
Thus if $\tau \ne 0$ , the $\dfrac{{dL}}{{dt}} \ne 0$ .(Change in angular momentum $\ne$ 0)
$\Rightarrow$ The angular momentum at B and O are not constant. This makes the options A and B false.
Now, we know that the particle begins its motion at A with velocity $v0$ . However, due to the tension on thread AB, the direction of velocity keeps changing. Thus, implying there is change in momentum due to change in velocity.
$\Rightarrow$ The momentum is not constant. Thus, making option C false.
Now, we can also observe that the Tension $T$ has not caused any work to be done, nor the system has dissipated any kind of energy. So, the kinetic energy of the system is constant.
$\Rightarrow$ The kinetic energy of the system is constant. Thus, making option D true.
The options that are not true among the ones provided are A, B, C.

Note
The torque $\tau = rmv\sin \theta$ is not necessary to find the existence of torque in the above problem. We know if a force causes a motion around a specific axis then that force is called torque. However, it was only used to introduce the relationship between angular momentum for a point object with linear momentum of the same object.