Question

A horizontal overhead power line carries a current of $90{\text{A}}$ in the east to west direction. Find the magnitude of the magnetic field due to the current $1.5{\text{m}}$ below the line.
A) $1.2{\text{T}}$
B) $1.2 \times {10^{ - 10}}{\text{T}}$
C) ${\text{0T}}$
D) $1.2 \times {10^{ - 5}}{\text{T}}$

Answer 1

The horizontal over head line carrying the given current can be considered as a conductor carrying the same amount of current. So the strength of the magnetic field at a point below the line will be proportional to the current in the line and it will be inversely proportional to the given distance below the line to the point.

Formula used:
The magnetic field due to a current-carrying conductor at a point P from the conductor is given by, $B = \dfrac{{{\mu _0}I}}{{2\pi r}}$ where ${\mu _0}$ is the permeability of free space, $I$ is the current through the conductor and $r$ is the perpendicular distance between the point and the conductor.

Complete step by step answer:
Step 1: Sketch a figure of the problem at hand.
The problem at hand involves a horizontal overhead line that carries some amount of current. The direction of the current is given to be from east to west. We have to determine the magnitude of the magnetic field at some distance below the given line. This is sketched in the figure below.

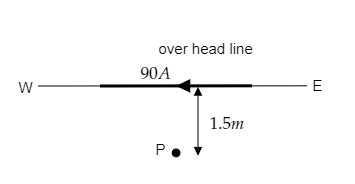
P is the point at which the magnetic field $B$ is to be determined.
The current in the line is given to be $I = 90{\text{A}}$.
The perpendicular distance between point P and the line is given to be $r = 1.5{\text{m}}$.
Step 2: Express the relation for the magnetic field at P.
As the line carrying the given current is similar to a conductor carrying the same current we have the magnetic field at P as $B = \dfrac{{{\mu _0}I}}{{2\pi r}}$ ------- (1)
Substituting for $I = 90{\text{A}}$ and $r = 1.5{\text{m}}$ in equation (1) we get,
$\Rightarrow B = \dfrac{{4\pi \times {{10}^{ - 7}} \times 90}}{{2\pi \times 1.5}} = 1.2 \times {10^{ - 5}}{\text{T}}$
Thus the magnitude of the magnetic field is obtained as
$\Rightarrow B = 1.2 \times {10^{ - 5}}{\text{T}}$.

Hence the correct option is D.

Note:
The direction of the magnetic field is determined using the right-hand thumb rule where the thumb of the right-hand points in the direction of the current i.e. from east to west and the fingers curl around the thumb in the direction of the magnetic field which will be perpendicularly out of the plane of the paper. This implies that the direction of the magnetic field is towards the south direction.