Question

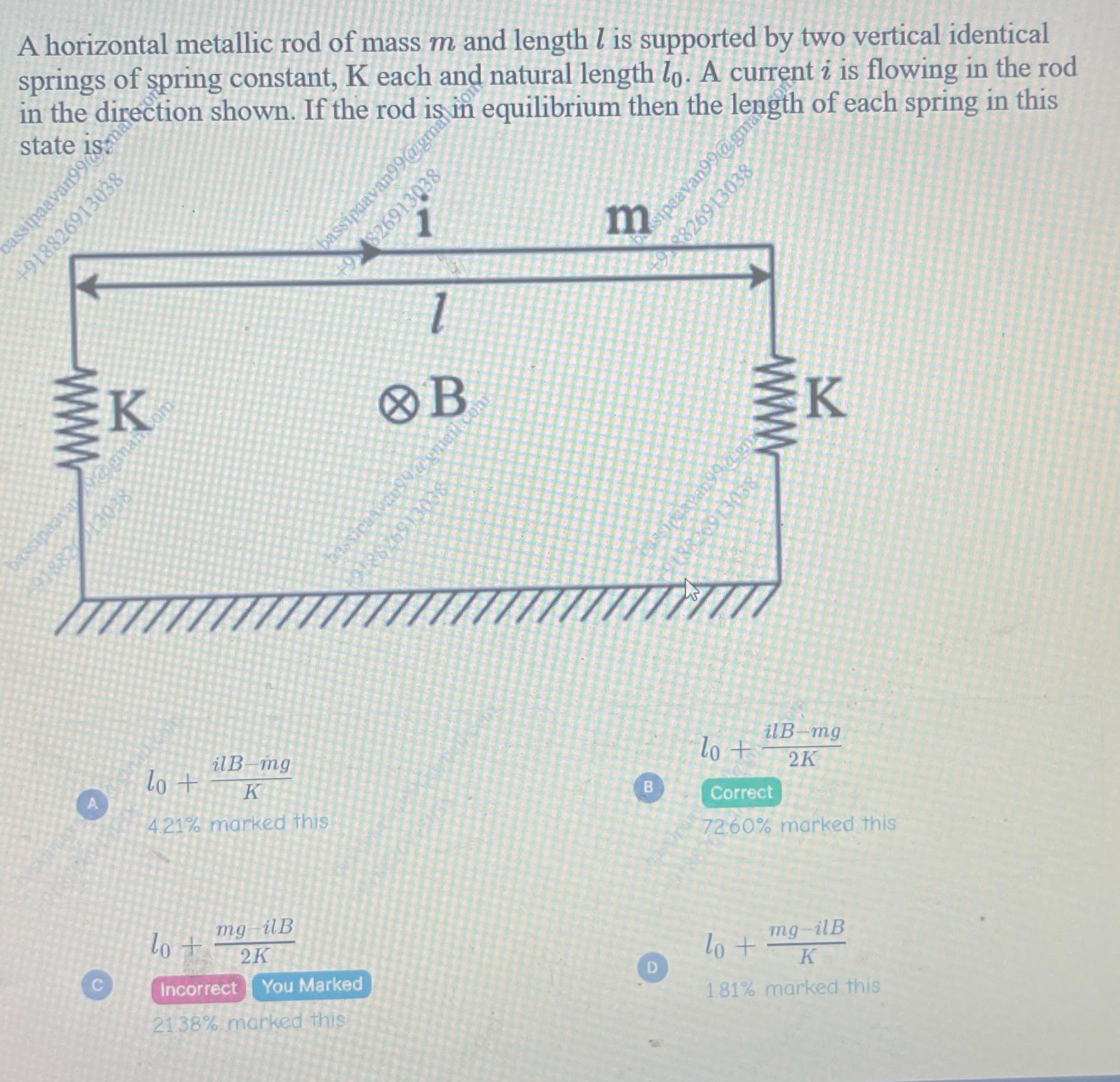
A horizontal metallic rod of mass $m$ and length $l$ is supported by two vertical identical springs of spring constant, K each and natural length $l_0$. A current $i$ is flowing in the rod in the direction shown. If the rod is in equilibrium then the length of each spring in this state is:

• A. $l_0 + \frac{ilB - mg}{K}$
• B. $l_0 + \frac{ilB - mg}{2K}$
• C. $l_0 + \frac{mg - ilB}{2K}$
• D. $l_0 + \frac{mg - ilB}{K}$

Answer 1

Answer: (B)

B. $l_0 + \frac{ilB - mg}{2K}$

Answer 2

Solution Explanation:

1. Write the force balance on the rod. In equilibrium, the total upward force from the two springs equals the net downward force. However, here the magnetic force acts upward (so it reduces the effective weight) so that   Upward spring force = Magnetic force – Weight
2. Since each spring with spring constant K is extended by Δl, the combined force is   2K·Δl = i lB – mg
3. Therefore, the extension of each spring is   Δl = (i lB – mg)/(2K)
4. The length of each spring in equilibrium is its natural length plus the extension, i.e.,   l₀ + (i lB – mg)/(2K)