Question

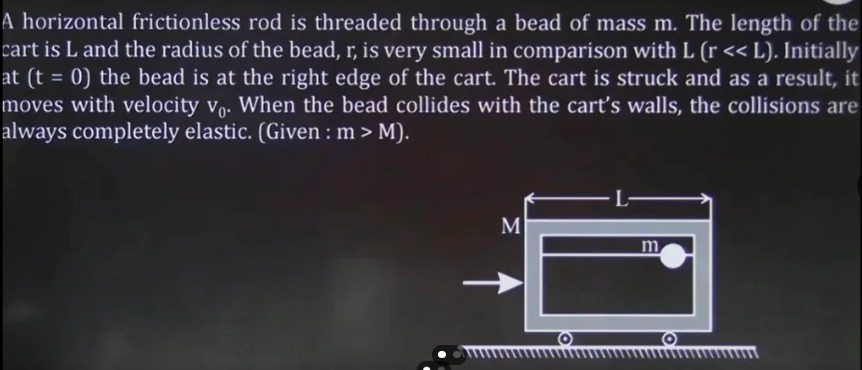
A horizontal frictionless rod is threaded through a bead of mass m. The length of the cart is L and the radius of the bead, r, is very small in comparison with L (r ≪ L). Initially at (t = 0) the bead is at the right edge of the cart. The cart is struck and as a result, it moves with velocity $v_0$. When the bead collides with the cart's walls, the collisions are always completely elastic. (Given : m > M).

Answer 1

The bead undergoes simple harmonic motion relative to the cart with angular frequency

$$\omega = \frac{\pi v_0}{L}\sqrt{\frac{M}{m}}.$$

Hence the time period of oscillation is

$$T = \frac{2\pi}{\omega} = \frac{2L}{v_0}\sqrt{\frac{m}{M}}.$$

Answer 2

Step 1: Frame transformation
Work in the rest frame of the cart’s centre of mass motion. In this frame the bead reflects elastically between two walls moving symmetrically.

Step 2: Effective spring analogy
Each elastic collision reverses the bead’s velocity relative to the cart and imparts impulse to the cart. For m ≫ M, the cart’s motion is small and the bead feels an effective restoring force proportional to its displacement.

Step 3: Small‑oscillation limit
Linearizing the motion yields simple harmonic motion with

$$\omega = \frac{\pi v_0}{L}\sqrt{\frac{M}{m}}\,.$$

Step 4: Time period

$$T = \frac{2\pi}{\omega} = \frac{2L}{v_0}\sqrt{\frac{m}{M}}.$$