Question

A horizontal frictionless rod is threaded through a bead of mass m. The length of the cart is L and the radius of the bead, r, is very small in comparison with L(r << L). Initially at (t = 0) the bead is at the right edge of the cart. The cart is struck and as a result, it moves with velocity ${{v}_{0}}$ towards right. When the bead collides with the cart’s walls, the collisions are completely elastic.

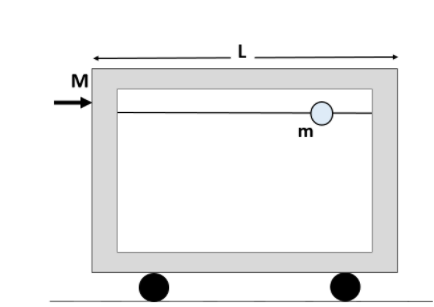
What is the velocity of the cart just after the first collision?
$\begin{aligned} & A)\dfrac{-m{{v}_{0}}}{m+M} \\\ & B)\dfrac{M{{v}_{0}}}{m+M} \\\ & C)\dfrac{M-m}{m+M}{{v}_{0}} \\\ & D)\dfrac{2M}{m+M}{{v}_{0}} \\\ \end{aligned}$

Answer 1

We will use the law of conservation of momentum to solve this equation. It states that the momentum of an isolated system remains constant. Here, the collision between the bead and walls of the cart is given as elastic. In elastic collisions, momentum is always conserved. The bead is at rest initially and we will solve for the velocity of the cart from the expression obtained from law of conservation of momentum. Also, we will use the concept of coefficient of restitution (e) to obtain a relation between the velocity of the bodies.

Formula Used:
$\begin{aligned} & {{m}_{1}}{{u}_{1}}+{{m}_{2}}{{u}_{2}}={{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}} \\\ & e=\left| \dfrac{{{V}_{{{2}_{final}}}}-{{V}_{{{1}_{final}}}}}{{{V}_{{{1}_{initial}}}}-{{V}_{{{2}_{initial}}}}} \right| \\\ \end{aligned}$

Complete step by step answer:
First of all, we will try to draw a diagram for understanding the situation.
Let us take the cart as a simple body for simplifying the diagram.

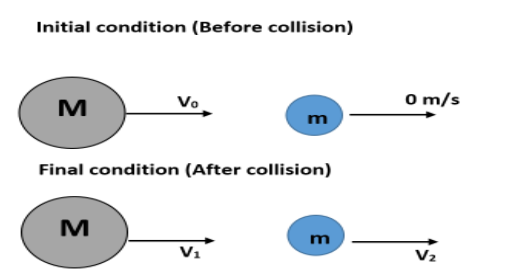
Here, M is the mass of the cart and m is the mass of the bead. The bead is initially at rest. Initial velocity of the cart is taken as ${{v}_{0}}$. After collision, let us assume that the car will be having a velocity of ${{v}_{1}}$ and the bead will be having a velocity of ${{v}_{2}}$.
So, according to law of conservation of momentum,
$\begin{aligned} & M{{v}_{0}}+m\times 0=M{{v}_{1}}+m{{v}_{2}} \\\ & \Rightarrow M{{v}_{0}}=M{{v}_{1}}+m{{v}_{2}} \\\ \end{aligned}$
Now, we will equate this expression and find the velocity of the cart.
Before that, we will find the relation between velocities using coefficient of restitution. For an elastic collision, e=1.
Therefore,

& e=\left| \dfrac{{{V}_{{{2}_{final}}}}-{{V}_{{{1}_{final}}}}}{{{V}_{{{1}_{initial}}}}-{{V}_{{{2}_{initial}}}}} \right|=1 \\\ & \Rightarrow {{v}_{0}}={{v}_{2}}-{{v}_{1}} \\\ \end{aligned}$$ From this relation, we can find ${{v}_{2}}$ as, $${{v}_{2}}={{v}_{1}}+{{v}_{0}}$$ Now, substituting this in the expression formed by momentum conservation, $$\begin{aligned} & \Rightarrow M{{v}_{0}}=M{{v}_{1}}+m\left( {{v}_{1}}+{{v}_{0}} \right) \\\ & \Rightarrow M{{v}_{0}}-m{{v}_{0}}=M{{v}_{1}}+m{{v}_{1}} \\\ & \Rightarrow {{v}_{0}}\left( M-m \right)={{v}_{1}}\left( M+m \right) \\\ & \Rightarrow {{v}_{1}}=\dfrac{\left( M-m \right)}{\left( M+m \right)}{{v}_{0}} \\\ \end{aligned}$$ Therefore, the velocity of the cart just after the first collision is found to be $${{v}_{1}}=\dfrac{\left( M-m \right)}{\left( M+m \right)}{{v}_{0}}$$. **So, option C is the right answer.** **Note:** Whenever we come up with this type of questions, it should be noted that in case of elastic collision, the momentum and energy will both be conserved and the coefficient of restitution will be 1. But in case of inelastic collision, there will be some loss of energy and final velocity of the body will depend on the masses and velocities of the bodies.