Question

A horizontal force $F = mg/3$ is applied on the upper surface of a uniform cube of mass $'m'$ and side $'a'$ which is resting on a rough horizontal surface having ${\mu _s} = 1/2$.The distance between line of action $'mg'$ and normal reaction $'N'$ is given as $a/x$. Find $x$

Answer 1

In this type of problem we use the concept of torque. Because in the above question there are couples of forces working together to rotate the body. torque is a vector quantity which has a tendency to rotate the body.
$\vec \Gamma = \vec r \times \vec F$.
Where $\vec \Gamma$=torque along the body
$\vec r$=position vector
$\vec F$=force on the body

Complete step by step answer:

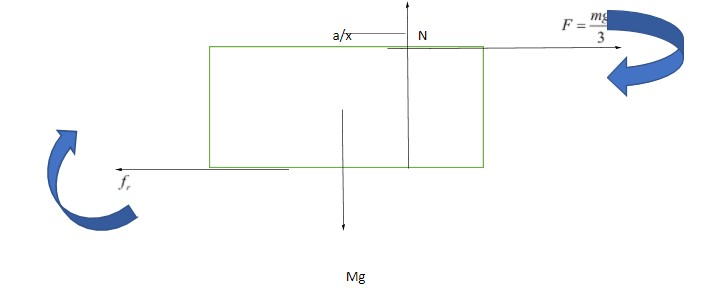
By the above figure we can say that the body has a tendency to rotate clockwise.
$\therefore$body does not have translatory motion hence applied force will be equal to friction force
Mathematically ${f_r} = \dfrac{{mg}}{3}$
So apply equilibrium condition on the body at point o which is at center of body.
We get,
$N \times \dfrac{a}{x} = \dfrac{{mg}}{3}\dfrac{a}{2} + {f_r} \times \dfrac{a}{2}$
Where N=normal reaction force
m = mass of the body
${f_r}$=friction force on the body
a=side of the rectangle
x=variable in the figure
now,
Putting value of ${f_r} = \dfrac{{mg}}{3}$
$N \times \dfrac{a}{x} = \dfrac{{mg}}{3}\dfrac{a}{2} + \dfrac{{mg}}{3}\dfrac{a}{2}$
$\therefore N = mg$
So, $mg \times \dfrac{a}{x} = \dfrac{{mg}}{3}a$
$\dfrac{a}{x} = \dfrac{a}{3}$
On comparing the above equation we get x=3.

Note:

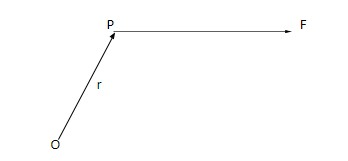
Consider a force $\vec F$ acting on a particle p. Choose an origin O and let $\vec r$ be the position vector of the particle experiencing the force. We define the torque of the force $\vec F$ about O as $\vec \Gamma = \vec r \times \vec F$
This vector quantity has its direction perpendicular to $\vec r$ and $\vec F$ according to the rule of cross product.