Question

A horizontal cylinder is fixed, its inner surface is smooth and its radius is $R$. A small block is initially at the lowest point. The minimum velocity that should be given to the block at the lowest point, so that it can just cross the point, P is $u$. Choose the correct option(s).

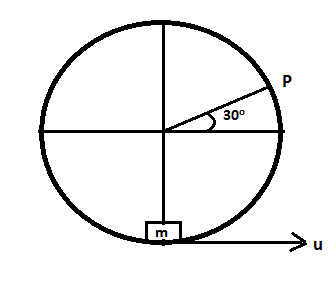
A.If the block moves anti-clockwise then $u = \sqrt {3.5gR}$
B.If the block moves anti-clockwise then $u = \sqrt {3gR}$
C.If the block moves clockwise then $u = \sqrt {3.5gR}$
D.If the block moves clockwise then $u = \sqrt {5gR}$

Answer 1

Here, we have to first calculate the angle moved by the mass to reach P in clockwise as well as anticlockwise direction. While reaching point P, the mass will experience the force due to gravity and the centripetal force. While solving we have to balance all these forces to get the desired answer.

Complete answer:
Now, first, we consider that the mass is moving in the anticlockwise direction as shown in the figure.

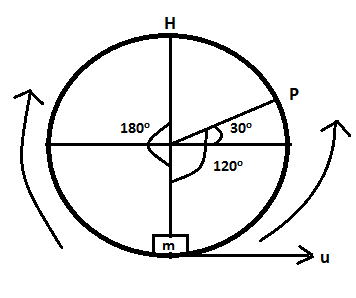
We observe here that if the mass moves in an anti-clockwise direction to reach point P, it moves $120^\circ$ from the lowest point. As it reaches point P, the centripetal force and the force due to gravity will act on it and balance the normal reaction on the mass. If the radius of the cylinder is $R$ and the velocity of the block is $u$ then resolving the forces we get,
$N = \dfrac{{m{u^2}}}{R} + mg(3\cos \theta - 2).......(1)$
Where,
$m$ is the mass of the block.
$R$ is the radius of the cylinder.
$N$ is the normal force.
$g$ is the acceleration due to gravity.
$\theta$ is the angle between the initial and final point of the block.
As the block of mass, $m$ reaches point P, its angle would be $120^\circ$ and the normal reaction $N$ would be zero. Substituting thevalues in equation (1), we get,
$\Rightarrow 0 = \dfrac{{m{u^2}}}{R} + mg(3\cos 120^\circ - 2)......(2)$
We know that, $\cos 120^\circ = - 0.5$ . So we get,
$\Rightarrow 0 = \dfrac{{m{u^2}}}{R} + mg\left( {\left( {3 \times - 0.5} \right) - 2} \right)$
$\Rightarrow 0 = \dfrac{{m{u^2}}}{R} + mg\left( { - 1.5 - 2} \right)$
$\Rightarrow 0 = \dfrac{{m{u^2}}}{R} - 3.5mg$
$\Rightarrow u = \sqrt {3.5gR}$
Now, if the block moves in the clockwise direction, it has to cross the highest point, H to reach point P. So the minimum velocity required by the block to reach point P is the same as the velocity required to cross point H. As, the block of mass, $m$ reaches point H, its angle would be $180^\circ$ and the normal reaction $N$ would again be zero as the forces are balanced. Substituting the values in equation (1), we get,
$\Rightarrow 0 = \dfrac{{m{u^2}}}{R} + mg(3\cos 180^\circ - 2)......(3)$
We know that, $\cos 180^\circ = - 1$ . So we get,
$\Rightarrow 0 = \dfrac{{m{u^2}}}{R} + mg\left( {\left( {3 \times - 1} \right) - 2} \right)$
$\Rightarrow 0 = \dfrac{{m{u^2}}}{R} + mg\left( { - 3 - 2} \right)$
$\Rightarrow 0 = \dfrac{{m{u^2}}}{R} - 5mg$
$\Rightarrow u = \sqrt {5gR}$

So, options A and D both are the correct answer.

Note:
There are two types of motion known to us. They are translational motion and rotational motion. The translational motion happens when all the points on the object move uniformly in the same direction. In rotational motion, the object rotates around a fixed axis. When an object shows both the rotational and translational motion, it is said to be experiencing the rolling motion. For example, when round stones fall from the top of the hill, the stones get rolling motion.