Question

A horizontal constant force is applied at vertical distance x from the center of a circular object $(M, R)$. If the coefficient of friction between the object and ground is $(\mu)$ and the object is under pure rolling then choose correct option(s).

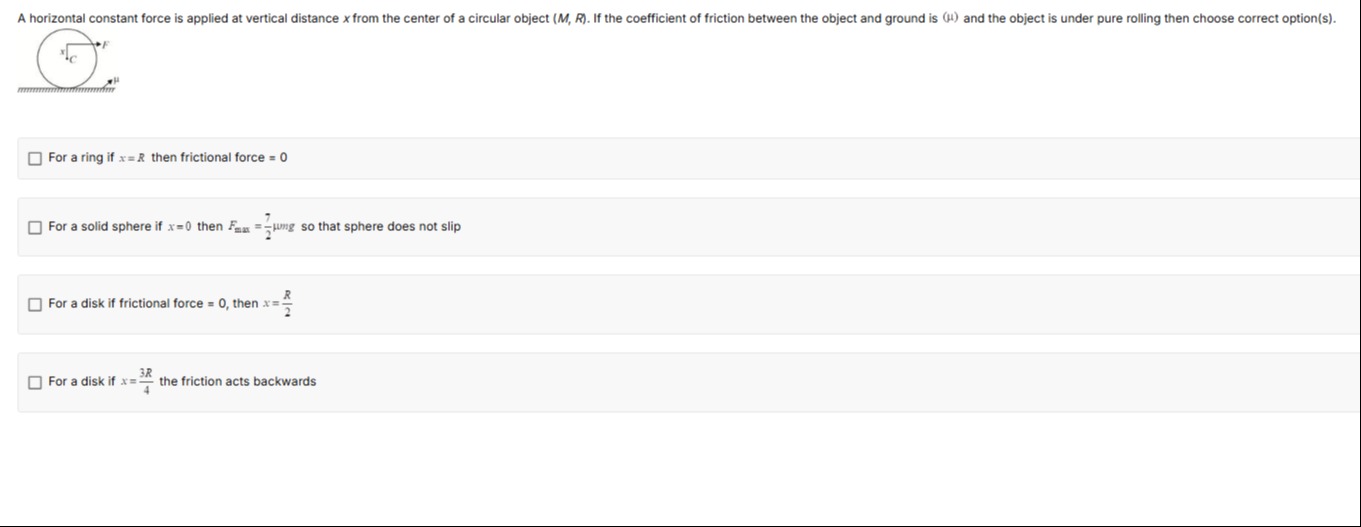
• A. For a ring if $x=R$ then frictional force = 0
• B. For a solid sphere if $x=0$ then $F_{max}=\frac{7}{2}\mu mg$ so that sphere does not slip
• C. For a disk if frictional force = 0, then $x=\frac{R}{2}$
• D. For a disk if $x=\frac{3R}{4}$ the friction acts backwards

Answer 1

Answer: (A), (B), (C)

Options 1, 2, and 3 are correct.

Answer 2

We start by writing the two equations for a body rolling without slipping under an applied horizontal force $F$ acting at a vertical distance $x$ from the center.

1. Translation:

   $m\,a = F + f$

   (where the sign of $f$ will be determined by its direction)

2. Rotation about the center:

   The torque due to $F$ is $F x$ and due to friction is $-fR$ (taking the “positive” sense consistent with rolling), so

   $I\,\alpha = F\,x - f\,R$

   Using the no–slip condition, $\alpha = \frac{a}{R}$, we get:

   $I\,\frac{a}{R} = F\,x - f\,R$

Now, solving for $f$:

• From translation:

  $a = \frac{F + f}{m}$

• Substituting into the rotation equation:

  $I\,\frac{F + f}{m\,R} = F\,x - f\,R$

Multiply through by $mR$:

$I\,(F + f) = mR\,(F\,x - f\,R)$

Rearrange to isolate $f$:

$I\,F + I\,f = mF\,x\,R - m\,f\,R^2$

$f\,(I + m\,R^2) = F\,(mR\,x - I)$

Thus,

$f = F\,\frac{mR\,x - I}{I + m\,R^2}$

Note that the sign of $f$ depends on the numerator $mR\,x - I$.

Now we analyze the options:

1. For a ring if $x = R$ then frictional force = 0:

   For a ring, $I = mR^2$. Then

   $x = \frac{I}{mR} = \frac{mR^2}{mR} = R$

   Thus, if $x = R$ then $mR\,R - mR^2 = 0$ and so $f = 0$.

   Option 1 is correct.

2. For a solid sphere if $x = 0$ then $F_{max}=\frac{7}{2}\mu mg$ so that sphere does not slip:

   For a solid sphere, $I = \frac{2}{5}mR^2$. For $x=0$,

   $f = F\,\frac{0 - \frac{2}{5}mR^2}{\frac{2}{5}mR^2+mR^2} = -F\,\frac{\frac{2}{5}mR^2}{\frac{7}{5}mR^2} = -\frac{2}{7}F$

   The negative sign shows that friction opposes the applied force $F$. The maximum friction available is $\mu mg$, so to avoid slipping we require

   $\frac{2}{7}F_{max} \le \mu mg \quad\Longrightarrow\quad F_{max} \le \frac{7}{2} \mu mg$

   Thus, the maximum force before slipping is indeed $\frac{7}{2}\mu mg$.

   Option 2 is correct.

3. For a disk if frictional force = 0, then $x=\frac{R}{2}$:

   For a disk, $I=\frac{1}{2}mR^2$. The frictionless condition requires:

   $mR\,x - I = 0 \quad\Longrightarrow\quad x=\frac{I}{mR}=\frac{\frac{1}{2}mR^2}{mR} = \frac{R}{2}$

   Option 3 is correct.

4. For a disk if $x=\frac{3R}{4}$ the friction acts backwards:

   Again for a disk, with $I=\frac{1}{2}mR^2$, substituting $x=\frac{3R}{4}$ gives:

   $mR\,x - I = mR\left(\frac{3R}{4}\right) - \frac{1}{2}mR^2 = \left(\frac{3}{4}-\frac{1}{2}\right)mR^2 = \frac{1}{4}mR^2$

   which is positive. Thus $f$ is positive, meaning it acts in the same direction as F (not backwards).

   Option 4 is incorrect.