Question

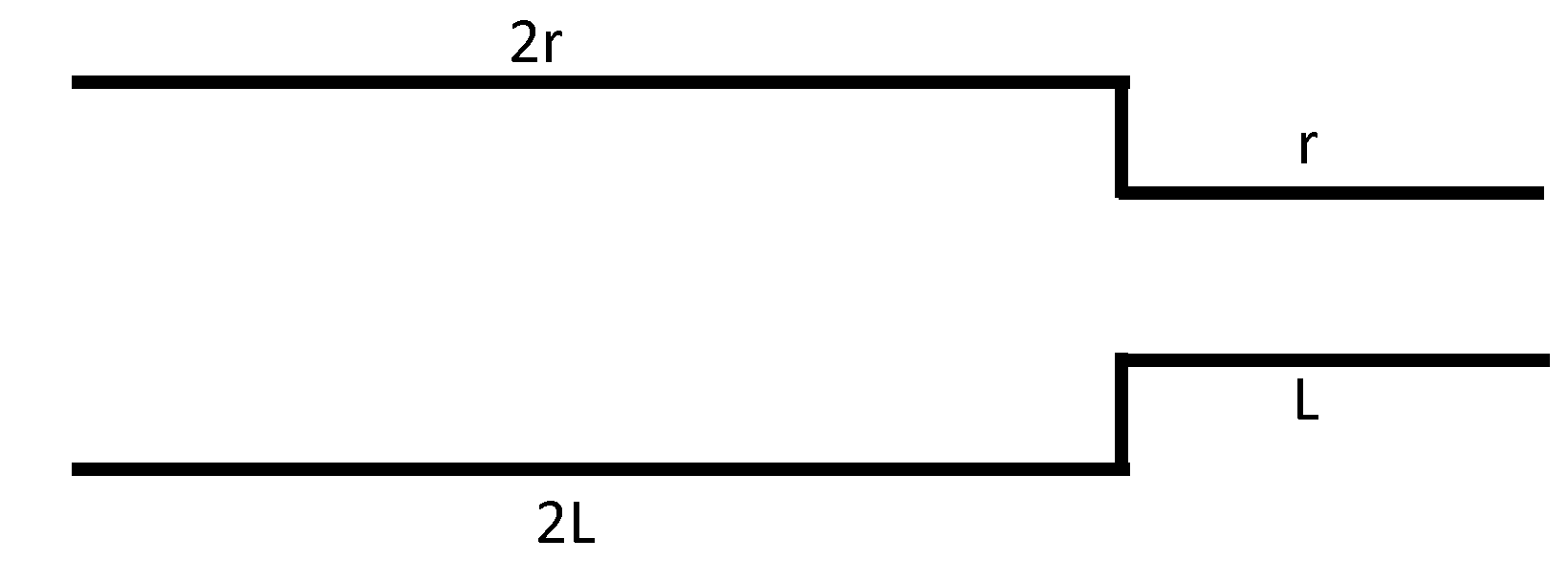
A horizontal composite capillary tube has a radius $2r$ for a length $2L$ and radius r for a length L as shown and is connected to a tank at one end and left free at the other end. The tank contains a liquid of coefficient of viscosity $\eta$. If a constant pressure difference P exists across the ends of the capillary tube, the volume flux through the capillary tube is

A. $\left( {\dfrac{{16}}{{17}}\dfrac{{\pi {{\Pr }^4}}}{{8\eta L}}} \right)$
B. $\left( {\dfrac{9}{8}\dfrac{{\pi {{\Pr }^4}}}{{8\eta L}}} \right)$
C. $\left( {\dfrac{{17}}{{16}}\dfrac{{\pi {{\Pr }^4}}}{{8\eta L}}} \right)$
D. $\left( {\dfrac{8}{9}\dfrac{{\pi {{\Pr }^4}}}{{8\eta L}}} \right)$

Answer 1

We know, by the equation of continuity, the rate of flow of liquids in both pipes will be the same. The value of flow rate is given by poiseuille formula.
1. poiseuille formula
Rate of flow of liquid, $Q = \dfrac{v}{t} = \dfrac{{\pi {{\Pr }^4}}}{{8nl}}$
Where l is the length of tube
R is the radius of tube
N is viscosity of fluid
P is pressure difference
V is volume, t is time taken

Complete step by step answer:
We know that, by poiseuille formula the volume of liquid flowing per second through a horizontal capillary tube of length l, radius r and pressure difference p is
$q = \dfrac{v}{t} = \dfrac{{\pi {{\Pr }^4}}}{{8nl}}$
Now, as both pipes are connected in the middle so, by the equation of continuity the rate of flow of both should be the same.
Let the pressure in the middle be P by equation of continuity,
$\dfrac{{\pi \left( {P - {P_1}} \right){r_1}^4}}{{8n{\text{ }}{{\text{l}}_1}}} = \dfrac{{\pi \left( {{P_1}} \right){r_2}^4}}{{8n{\text{ }}{{\text{l}}_2}}}$
Where ${r_1} = 2\mu ,{\text{ }}\mu {\text{ = 2L}}$
${r_2} = r,{\text{ }}{{\text{l}}_2} = L$
As given in question,
So, we have
$\dfrac{{\pi \left( {P - {P_1}} \right){{\left( {2r} \right)}^4}}}{{8x\left( {2L} \right)}} = \dfrac{{\pi {P_1}{r^4}}}{{8{n^L}}} \\\ \Rightarrow \dfrac{{\left( {P - {P_1}16{r^4}} \right)}}{{2L}} = \dfrac{{{P_1}{r^4}}}{L} \\\ \Rightarrow \dfrac{{\left( {P - {P_1}} \right)16}}{2} = {P_1} \\\ \Rightarrow 8P - 8{P_1} = {P_1} \\\ \Rightarrow 8P = 9{P_1} \\\ \Rightarrow {P_1} = \dfrac{{8P}}{q} \\\$
Now, the volume flux through the capillary tube $= \dfrac{{\pi {P_1}{r^4}}}{{8nL}}$
$= \dfrac{{\pi 8{{\Pr }^4}}}{{9 \times 8nL}} \\\ = \dfrac{8}{9}\dfrac{{\pi {{\Pr }^4}}}{{8nL}} \\\$

So, the correct answer is “Option D”.

Note:
As at middle, the pressure is P, so, for tube of length $2L$, the pressure difference is $P - {P_1}$, and for tube of length ${L_1}$ the pressure difference is ${P_1}$ as its other end is open.