Solveeit Logo
Login

Question

Question: A hoop rolls on a horizontal ground without slipping with linear speed \( v \) . Speed of a particle...

A hoop rolls on a horizontal ground without slipping with linear speed vv . Speed of a particle P on the circumference of the hoop at an angle θ\theta is:

A. 2vsin⁡(θ2)2v\sin \left( {\dfrac{\theta }{2}} \right)
B. vsin⁡θv\sin \theta
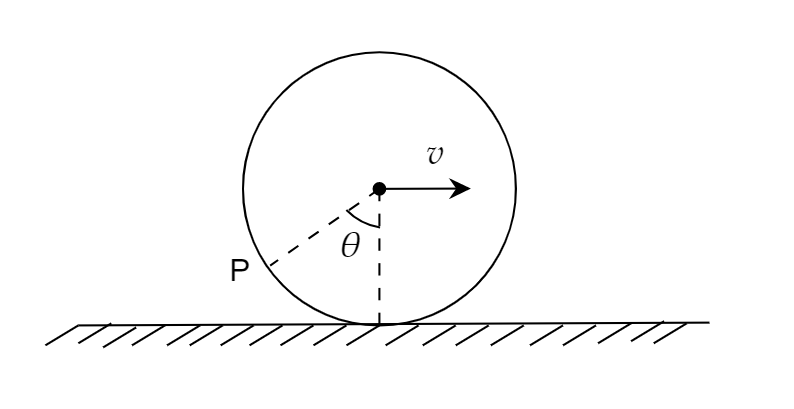
C. 2vcos⁡(θ2)2v\cos \left( {\dfrac{\theta }{2}} \right)
D. vcos⁡θv\cos \theta

Explanation

Solution

In the given question, the particle is in rolling motion. At point P it will have both angular velocity and linear velocity, we have to find the resultant velocity from that point. By formulating and comparing equations we will find the answer.

Complete step by step solution:
According to the question, the hoop is in rolling motion on the horizontal ground without slipping. So, at point P the hoop is moving with both linear velocity vv and angular velocity vv .
The direction of the angular velocity is tangential to the point at which it acts.

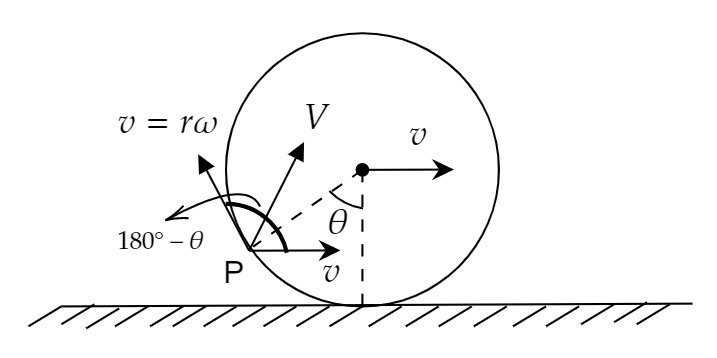
Let the speed of the particle be VV and the angle between the angular velocity and linear velocity is 180∘−θ{180^ \circ } - \theta .
From parallelogram law of vector, we get the speed of the particle as,
V=v2+v2+2.v.vcos⁡(180∘−θ)V = \sqrt {{v^2} + {v^2} + 2.v.v\cos \left( {{{180}^ \circ } - \theta } \right)}
Simplifying the given equation we get,
V=2v2−2v2cos⁡θV = \sqrt {2{v^2} - 2{v^2}\cos \theta }
Now, taking 2v22{v^2} as common we get,
V=2v2(1−cos⁡θ)V = \sqrt {2{v^2}\left( {1 - \cos \theta } \right)}
Now, taking 2v22{v^2} out of the square root, we get,
V=2v(1−cos⁡θ)V = \sqrt 2 v\sqrt {\left( {1 - \cos \theta } \right)}
From Trigonometric half angle formula, we know that 1−cos⁡θ=2sin⁡2θ21 - \cos \theta = 2{\sin ^2}\dfrac{\theta }{2}
Substituting its value we get,
V=2v2sin⁡2θ2V = \sqrt 2 v\sqrt {2{{\sin }^2}\dfrac{\theta }{2}}
Hence, V=2vsin⁡θ2V = 2v\sin \dfrac{\theta }{2}
The correct option is A. 2vsin⁡(θ2)2v\sin \left( {\dfrac{\theta }{2}} \right) .

Note:
It must be noted that as the surface is frictionless, so the angular velocity at point P and linear velocity are equal. If the surface had friction, then the angular velocity and linear velocity will not be the same. The angle between the two vectors is found from the parallelogram as we extend the velocity direction.