Question

A homogeneous solid cylindrical roller of radius $R$ and mass $M$ is pulled on a cricket pitch by a horizontal force. Assuming rolling without slipping, angular acceleration of the cylinder is _____?
(A) $\dfrac{{3F}}{{2mR}}$
(B) $\dfrac{F}{{3mR}}$
(C) $\dfrac{{2F}}{{3mR}}$
(D) $\dfrac{F}{{2mR}}$

Answer 1

Hint From the formula for torque given by product of the moment of inertia and the angular acceleration. The torque is also given by the product of the force and the radius. So equating we get the angular acceleration.
In this solution we will be using the following formula,
$\Rightarrow \tau = I\alpha$
where $\tau$ is the torque, $I$ is the moment of inertia and $\alpha$ is the angular acceleration.
again $\tau = FR$
where $F$ is the force and $R$ is the distance from the axis of rotation.

Complete step by step answer
In the question we are given a homogeneous solid cylinder that is given a horizontal force. So we can draw the diagram as,

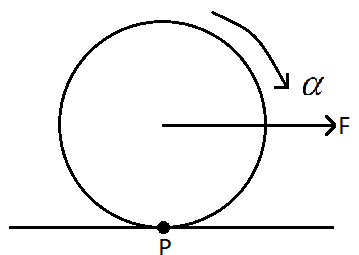
The cylinder, as we can see from the diagram, is touching at the point P. Now the torque is given as the product of the moment of inertia and the angular acceleration. So we can write,
$\Rightarrow \tau = I\alpha$
Now the moment of inertia of a solid homogeneous cylinder about an axis passing through its center and along the length is given by the formula,
$\Rightarrow I = \dfrac{3}{2}M{R^2}$
So substituting this we get,
$\Rightarrow \tau = \dfrac{3}{2}M{R^2}\alpha$
Now the torque on the cylinder due to the force that is acting on it horizontally is given by the product of the force and the distance of the point of contact from the axis of rotation. Hence we have,
$\Rightarrow \tau = FR$
So we can equate the two values of torque as,
$\Rightarrow \dfrac{3}{2}M{R^2}\alpha = FR$
Keeping only the $\alpha$ in the LHS and taking the rest of the terms to the RHS we get,
$\Rightarrow \alpha = \dfrac{2}{{3M{R^2}}}FR$
On cancelling the $R$ from the numerator and the denominator we get,
$\Rightarrow \alpha = \dfrac{{2F}}{{3MR}}$
Hence the angular acceleration is $\dfrac{{2F}}{{3MR}}$
So the correct answer is option (C).

Note
The moment of inertia of a rigid body is the quantity that determines the torque needed for the required angular acceleration about a rotational axis. It is equivalent to the way mass determines the force needed for desired acceleration.