Question

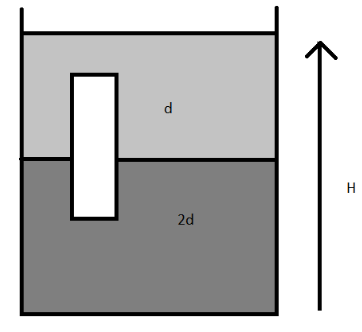
A homogeneous solid cylinder of length L $(Less Than\dfrac{H}{2})$ , cross sectional area A is immersed such that it floats with its axis vertical at the liquid-liquid interface with length $\dfrac{L}{4}$ in the density liquid as shown in the figure. The lower density liquid is open to atmosphere having pressure ${P_0}$ .then, density D of solid is given by

A.\dfrac{5}{4}d \\\
B.\dfrac{4}{5}d \\\
C.4d \\\
D.$\dfrac{d}{5} \\\$

Answer 1

Hint : Here if we consider the vertical equilibrium of the cylinder, weight of the cylinder is equal to the developed upthrust due to upper liquid and the upthrust due to the lower liquid. Weight of two liquids displaced is equal to the right of the block.

Complete Step By Step Answer:
According to the law of floatation, weight of the block is equal to the weight of the liquid displaced.
Here in the given question;
Weight of two liquids displaced is equal to the right of the block.
Weight of the block is equal to $LADg$
Weight of the first liquid is $\dfrac{L}{4}A(2d)g$ .
Weight of the second liquid is $\dfrac{{3L}}{4}Adg$ .
Now;
LADg = \dfrac{L}{4}A(2d)g + \dfrac{{3L}}{4}Adg \\\ \Rightarrow D = \dfrac{1}{2}d + \dfrac{3}{4}d = \dfrac{5}{4}d \\\
Hence, the density of the given solid is $\dfrac{5}{4}d$ .
Option A is the correct answer.

Note :
Law of flotation – when anybody displaces a weight of water equal to the weight of itself, it starts floating. This is called the principle of flotation and Archimedes principle equates that the above equation as buoyant force to the weight of the fluid displaced.
Weight of two liquids displaced is equal to the right of the block. Weight of the cylinder is equal to the developed upthrust due to upper liquid and the upthrust due to the lower liquid.