Question

A hollow straight tube of length $l$ and mass $m$ can turn freely about its centre on a smooth horizontal table. Another smooth uniform rod of the same length and mass is fitted into the tube so that their centers coincide. The system is set in motion with an initial angular velocity ${\omega _0}$ . The angular velocity of the rod at an instant when the rod slips out of the tube is
(A) ${\omega _0}/3$
(B) ${\omega _0}/2$
(C) ${\omega _0}/4$
(D) ${\omega _0}/7$

Answer 1

Hint
To solve this question, we need to use the principle of conservation of angular momentum. For that, we need to find the moment of inertia of the system for the initial and final states.
$\Rightarrow I = \dfrac{{m{l^2}}}{{12}}$ , where $I$ is the moment of inertia of a rectangular body of mass $m$ and length $l$ about an axis passing through its centre of gravity.

Complete step by step answer
Let the required angular velocity be $\omega$
The initial situation is shown in the figure below.

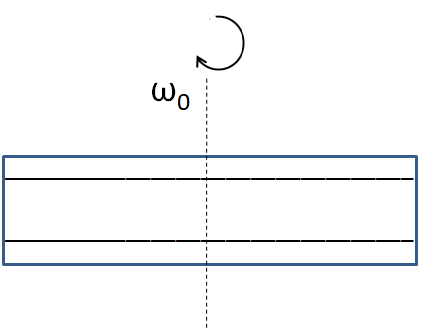
We know that the moment of inertia of a rod of length $l$ and mass $m$ , about an axis passing through its centre of gravity is $I = \dfrac{{m{l^2}}}{{12}}$
Now the hollow tube is completely covering the rod. So they can together be considered as one single rod of length $l$ and mass $m + m = 2m$
So the moment of inertia of the system about the given axis is
$\Rightarrow {I_1} = \dfrac{{2m{l^2}}}{{12}}$
$\Rightarrow {I_1} = \dfrac{{m{l^2}}}{6}$
Since the initial angular velocity of the system is ${\omega _0}$ , so the initial angular momentum of the system is
$\Rightarrow {L_1} = {I_1}{\omega _0}$
$\Rightarrow {L_1} = \dfrac{{m{l^2}}}{6}{\omega _0}$
The final situation, when the rod slips out of the hollow tube, is shown in the figure.

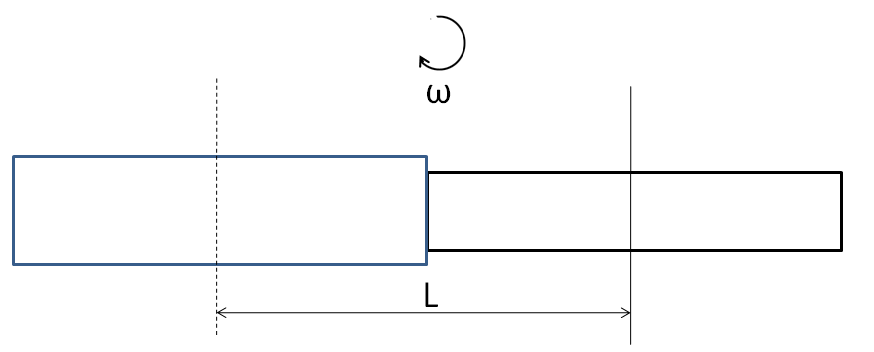
Now, the moment of inertia of the hollow tube about the original axis is
$\Rightarrow {I_{tube}} = \dfrac{{m{l^2}}}{{12}}$
And the moment of inertia of the rod about the original axis can be found by using parallel axis theorem
$\Rightarrow {I_{rod}} = \dfrac{{m{l^2}}}{{12}} + m{l^2}$
So, the moment of inertia of the rod + tube system about the original axis is
$\Rightarrow {I_2} = {I_{tube}} + {I_{rod}}$
$\Rightarrow {I_2} = \dfrac{{m{l^2}}}{{12}} + \left( {\dfrac{{m{l^2}}}{{12}} + m{l^2}} \right)$
On taking the LCM, we get
$\Rightarrow {I_2} = \dfrac{{m{l^2} + m{l^2} + 12m{l^2}}}{{12}}$
$\Rightarrow {I_2} = \dfrac{{14m{l^2}}}{{12}}$
Dividing numerator and denominator by 2, we get
$\Rightarrow {I_2} = \dfrac{{7m{l^2}}}{6}$
Also, since the final angular velocity is assumed to be $\omega$ , so the final angular momentum of the system is
$\Rightarrow {L_2} = {I_2}\omega$
$\Rightarrow {L_2} = \dfrac{{7m{l^2}}}{6}\omega$
Now, since there is no external torque is applied on this system, so according to the principle of conservation of angular momentum,
$\Rightarrow {L_1} = {L_2}$
Substituting the values of ${L_1}\& {L_2}$ found above
$\Rightarrow \dfrac{{m{l^2}}}{6}{\omega _0} = \dfrac{{7m{l^2}}}{6}\omega$
Dividing by $\dfrac{{m{l^2}}}{6}$ both sides, we get
$\Rightarrow {\omega _0} = 7\omega$
Finally, we get
$\Rightarrow \omega = \dfrac{{{\omega _0}}}{7}$
So, the final angular velocity of the rod when it slips out of the tube is $\dfrac{{{\omega _0}}}{7}$
Hence, the correct answer is option (D), $\dfrac{{{\omega _0}}}{7}$.

Note
We may argue what is causing the rod to lip out of the tube. The rod is slipping due to the centrifugal force which acts on the rod in the radial direction outwards the circle of rotation. As the tube is smooth, there is no friction to prevent the relative motion between the rod and the hollow tube, making the rod slip out of the tube.