Question
Question: A hollow sphere of mass \(M = 50kg\) and radius \(r = {\left( {\dfrac{3}{{40\pi }}} \right)^{\dfrac{...
A hollow sphere of mass M=50kg and radius r=(40π3)31m is immersed in a tank of water (ρw=103kg/m3) . The sphere is tied to the bottom of a tank by two wires A and B as shown in figure. Tension in wire A is (g=10m/s2))
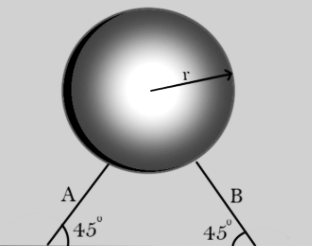
a. 1252N
b. 125N
c. 2502N
d. 250N
Solution
The hollow sphere will experience a buoyant force acting upward due to the liquid. The gravitational force and tension of the wire pulls the sphere downwards.
Step by step solution:
First we'll make a free body diagram of the sphere for better understanding.
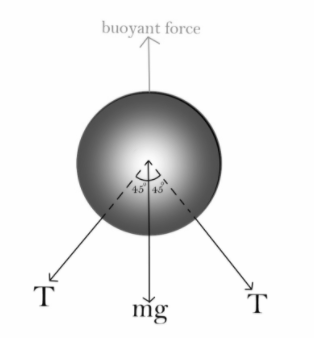
On balancing the forces, we get
Buoyant force=mg+Tsin45+Tsin45
Vρg=mg+2Tsin45
34πr3×ρ×g=mg+2T
34π(340π3)3×1000×10=(50)(10)+2T
T=2502N
Hence option c is correct
The sin component of the tension of both wires cancels each other.
Additional information:
- Buoyant force is an upward force exerted by any fluid that opposes the weight of partially or fully immersed fluid. As we go deeper and deeper in a fluid column, the pressure increases. Thus the pressure at the bottom of a column of fluid is greater than the top of the column. The pressure difference results in net upward force on any object which is partially or fully immersed in a fluid.
- If the density of the object is greater than the density of liquid in which it is immersed then the object will sink. If the density of object and fluid are equal then the object will remain suspended in fluid. On the other hand if the density of the object is less than that of fluid, then the object will float.
Note: Please remember that the buoyant force exerted by liquid depends on the density of the liquid itself and not on the density of fluid.
