Question
Question: A hollow sphere is moving with linear velocity and angular velocity as shown in figure. The time aft...
A hollow sphere is moving with linear velocity and angular velocity as shown in figure. The time after which pure rolling starts is :
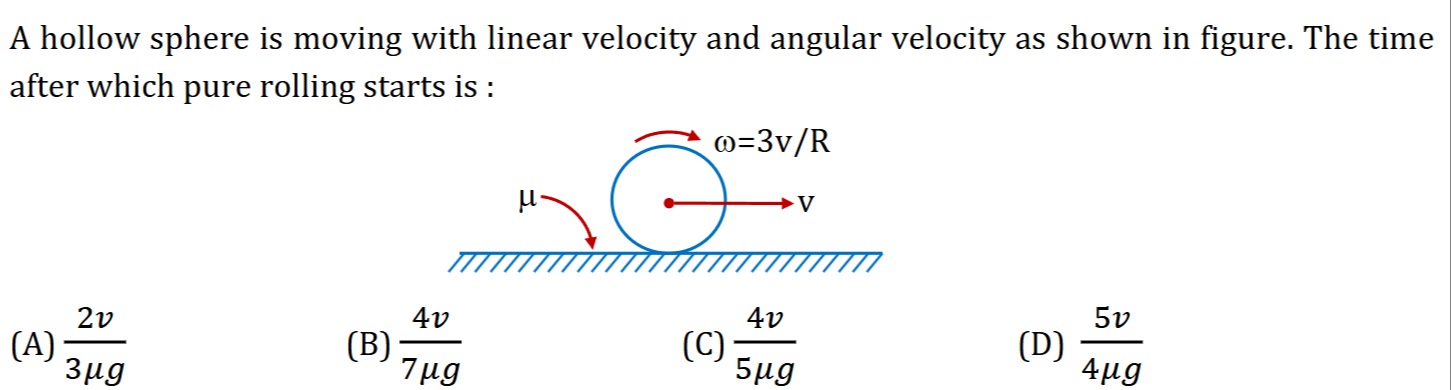
3μg2v
7μg4v
5μg4v
4μg5v
4v/5\mu g
Solution
Explanation of the solution:
-
Identify Initial State: The hollow sphere has initial linear velocity
v(right) and angular velocityω = 3v/R(clockwise). -
Determine Point of Contact Velocity: Let right be positive for linear velocity and counter-clockwise be positive for angular velocity. So,
v_cm = vandω_0 = -3v/R. The velocity of the point of contactv_P = v_cm - ωR = v - (-3v/R)R = 4v. Sincev_P > 0, the point of contact slides to the right. -
Apply Friction: Friction
f_k = μmgacts to the left on the sphere, opposing the sliding motion. -
Linear Motion Equations:
- Acceleration
a_cm = -f_k/m = -μg. - Linear velocity
v_cm(t) = v - μgt.
- Acceleration
-
Rotational Motion Equations:
- Moment of inertia for a hollow sphere
I = (2/3)MR^2. - Torque
τ = f_k R = μmgR. This torque is counter-clockwise (positive). - Angular acceleration
α = τ/I = (μmgR) / ((2/3)MR^2) = (3/2)(μg/R). - Angular velocity
ω(t) = ω_0 + αt = -3v/R + (3/2)(μg/R)t.
- Moment of inertia for a hollow sphere
-
Pure Rolling Condition: Pure rolling occurs when
v_cm(t) = ω(t)R.v - μgt = R(-3v/R + (3/2)(μg/R)t)v - μgt = -3v + (3/2)μgt4v = (1 + 3/2)μgt = (5/2)μgtt = (8v)/(5μg).
-
Reconciliation with Options: The calculated result
(8v)/(5μg)does not match any option. However, if the initial angular velocityω=3v/Rwas interpreted as counter-clockwise (i.e., in the direction of forward rolling), then:v_cm = v,ω_0 = 3v/R.v_P = v_cm - ωR = v - (3v/R)R = -2v. The point of contact slides to the left.- Friction
f_k = μmgacts to the right. a_cm = μg.v_cm(t) = v + μgt.- Torque
τ = -f_k R = -μmgR(clockwise, negative). α = τ/I = (-μmgR) / ((2/3)MR^2) = -(3/2)(μg/R).ω(t) = ω_0 + αt = 3v/R - (3/2)(μg/R)t.- Pure rolling:
v_cm(t) = ω(t)R. v + μgt = R(3v/R - (3/2)(μg/R)t)v + μgt = 3v - (3/2)μgt(1 + 3/2)μgt = 3v - v(5/2)μgt = 2vt = (4v)/(5μg). This matches option (C).
Given the options, it is highly probable that the intended angular velocity direction was counter-clockwise, despite the diagram showing it as clockwise.
