Question

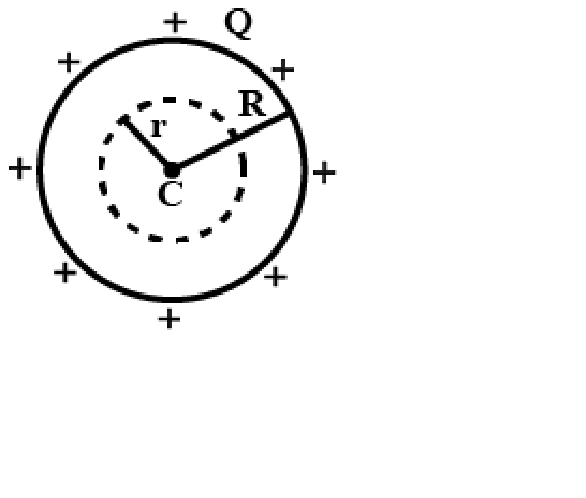
A hollow metal sphere of radius $R$ is uniformly charged. The electric field due to the sphere at a distance $r$ from the center.
A) Increases as $r$ increases for $r < R$ and for $r > R$ .
B) Zero as $r$ increases for $r < R$ , decreases as $r$ increases for $r > R$ .
C) Zero as $r$ increases for $r < R$ , increases as $r$ increases for $r > R$ .
D) Decreases as $r$ increases for $r < R$ and for $r > R$ .

Answer 1

We can use Gauss Law to solve this problem, because Gauss Law can be stated using the electric field. Charge is distributed over the surface of a hollow metal sphere. Take both the hollow metal sphere into consideration, i.e., inside, and outside, for getting the correct answer.
Formula used:
${{\phi }_{e}}=\oint{\overrightarrow{E}.\overrightarrow{dA}=\dfrac{Q}{{{\varepsilon }_{o}}}}$, where $E$ is the electric field,
$dA$ is a vector representing an infinitesimal element of area of the surface,
$Q$ is the total charge enclosed within volume, and
${{\varepsilon }_{o}}$ is the electric constant.

Complete answer:


According to Gauss Law, the net flux through any closed surface equals the total charge inside that surface divided by ${{\varepsilon }_{o}}$ . The equation for this law can be written as:
${{\phi }_{e}}=\oint{\overrightarrow{E}.\overrightarrow{dA}=\dfrac{{{Q}_{net}}}{{{\varepsilon }_{o}}}}$
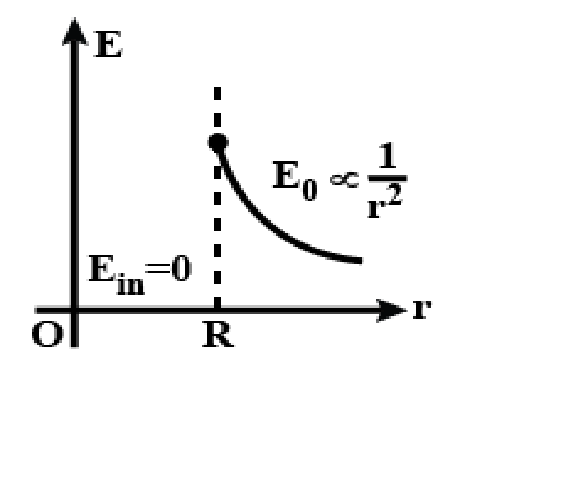
For rBy Gauss law, $${{\phi }_{e}}=\oint{{{\overrightarrow{E}}_{in}}.\overrightarrow{dA}=\dfrac{{{Q}_{net}}}{{{\varepsilon }_{o}}}=0\,(\because {{Q}_{net}}=0)}$$ \Rightarrow {{E}{in}}=0$For$r>R(outside sphere): By Gauss Law, $${{\phi }_{e}}=\oint{{{\overrightarrow{E}}_{o}}.\overrightarrow{dA}=\dfrac{{{q}_{en}}}{{{\varepsilon }_{o}}}}$$ Here,{{q}{en}}=Q,and,dA=4\pi {{r}^{2}}$Substitute the value in the above equation, we get:$\begin{aligned}
& \Rightarrow {{E}{o}}\times 4\pi {{r}^{2}}=\dfrac{Q}{{{\varepsilon }{o}}} \\
& \Rightarrow {{E}_{o}}\propto \dfrac{1}{{{r}^{2}}} \\
\end{aligned}$From the above solution, it is clear that the electric field is zero as$r$increases for$r < R$and decreases as$r$increases for$r > R$.

Therefore, the correct answer is Option (B).

Note:
Substitute the value properly in both the condition to get the final relation. It is necessary to derive both the relations before marking the result, so that we can get the dependency of the electric field, which will help to reach a solution.