Question
Question: A hollow metal pipe of length L is closed at one end and produces resonance when sounded with a tuni...
A hollow metal pipe of length L is closed at one end and produces resonance when sounded with a tuning fork of frequency n. The entire tube is then heated carefully so that at equilibrium temperature its length changes by l. If the changes in velocity V of the sound are v, then the resonance will occur with a tuning fork of frequency
A. 4(L+l)V+v
B. 2(L−l)V+v
C. 4(L+l)V−v
D. 4(L−l)V−v
Solution
Hint : A tuning fork is a fork-shaped acoustic resonator used in many applications to produce an increase in the sound pressure in an acoustic field at a particular frequency. The main reason for using the fork shape as it produces a very pure tone, with most of the vibration energy at the natural frequency.
Complete Step By Step Answer:
It is given that a hollow metallic tube of length L is closed at one end .Metallic tube produces vibration with a tuning fork of frequency n. So we can say that:
Metallic tube length= L
Frequency= n
Velocity = V
Since the temperature of the metallic pipe is increasing so its length also increases and its new length Lnew becomes L+l
Now we will consider the effect of temperature on the speed of sound. When the entire metallic tube is heated then temperature of the pipe increases the air molecules have more kinetic energy which increases the speed of the sound. Now new speed is Vnew becomes V+v
Now, we can find out the resonance produced by tuning the fork frequency.
Frequency for the first case when the metallic tube is closed at one end.
F=λV
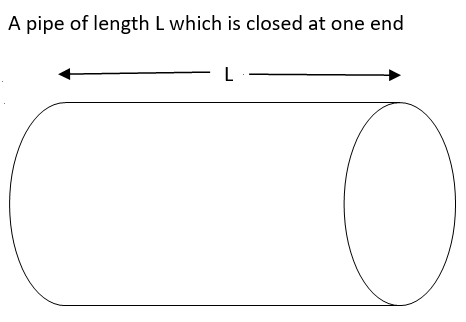
4λ=L
λ=4L F=4LV F=n
As given in question frequency is equal to n
Frequency for second case when temperature increases in that case L=L+l, V=V+v, now new frequency equal to
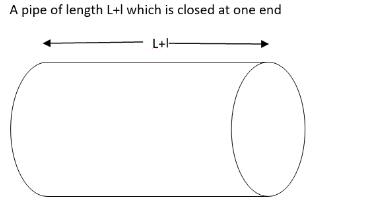
F′=λ′V+v F′=4(L+l)V+v
The changes in velocity V of the sound are v to V+v then the resonance will occur with a tuning fork of frequency is F′=4(L+L)V+v .
So, the correct answer is A.
Note :
Produces resonance when sounded with a tuning fork of frequency n means the system amplifies sound waves whose frequency equals one of its own natural frequencies of vibration.
