Question
Question: A hollow dielectric sphere with charge q which is uniformly distributed in its volume. Electric fiel...
A hollow dielectric sphere with charge q which is uniformly distributed in its volume. Electric field at point P which is r distance away from centre is
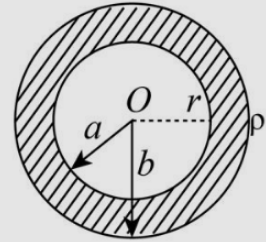
A. r2kq[b3−a3r3−a3]
B. r2kq[r3−a3b3−a3]
C. r2kq[r3−a3r3−a3]
D. Zero
Solution
The above problem can be resolved using the electric field concept and application for a spherical surface. The electric field at any spherical surface is expressed by utilizing the volume charge density and the magnitude of the charge on the surface. Moreover, by applying the standard formula for the electric field and substituting the values, one can obtain a simplified relationship for the electric field's magnitude for any spherical surface.
Complete step by step answer:
If ρ be the volume charge density. Then the magnitude of charge is given as,
Q=ρ×34π(b3−a3)...........................(1)
Let E is the magnitude of the electric field.
Then apply the Gauss’s law as,
E×4πr2=εQ
Here, r is the distance from centre and εis the permittivity of dielectric medium,
Solve by substituting the value of equation 1 in the above expression.
Therefore, the magnitude of electric field is r2kQ(b3−a3r3−a3) and option (A) is correct.
Note: To resolve the above problem, one must understand the concepts and the fundamentals of the gauss law and the importance of the gaussian surfaces. The gauss law can be applied to calculate the electric field's magnitude and variation of the electric field's magnitude by changing the position. Moreover, the magnitude of the electric field is different for the different shapes, but the exact calculation depends on the Gaussian surface analysis. Furthermore, the electric field's magnitude is calculated by considering charges on the surfaces and through the charge densities.
